Представление САР в виде структурной схемы. Линеаризация дифференциальных уравнений элементов системы
Глава 2. Методы математического описания элементов САР
Прочие классификации САР
Классификация САР по характеру работы исполнительного механизма
Классификация САР по статическим характеристикам системы
Классификация САР по характеру изменения задающего воздействия
Классификация систем автоматического регулирования (управления)
Системы регулирования разделяются на два основных класса :
1. Системы, выполняющие работу по заранее заданному закону (программе) вне зависимости от условий протекания технологического процесса. В этих системах информация о выходных величинах или отсутствует, или имеет второстепенное значение. Эти системы называют циклическими или детерминированными. По этой схеме работают автоматические поточные линии (прокатные станы, волочильные линии и т.п.), к ним же можно отнести и устройства робототехники, работающие по заданной программе. Это разомкнутые системы.
2. Системы, работающие с учетом фактического протекания процесса на основе информации об его работе и выходных величин. Такие системы называют информационными. Это замкнутые системы. К информационным системам относятся и САР тепловых процессов.
Информационные системы автоматического регулирования, в свою очередь, можно классифицировать по следующим основным признакам:
1) по принципу регулирования;
2) характеру изменения задающего воздействия;
3) статическим характеристикам;
4) характеру работы исполнительного механизма;
5) виду дифференциального уравнения, описывающего динамику системы;
6) в зависимости от числа входных и выходных величин.
1.3.1. Классификация САР по принципу регулирования:
§ принцип Ползунова – Уатта,
§ принцип Понсèле,
§ комбинированный принцип.
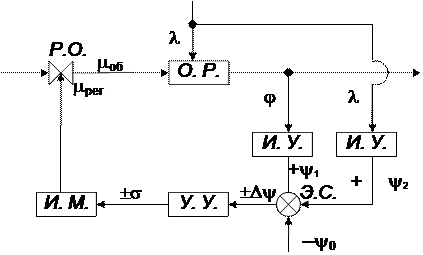
Принцип Ползунова – Уатта. Его называют принципом сравнения или принципом регулирования по отклонению регулируемой величины от заданного значения. Структурная схема этого принципа представлена на рис. 1.3. Достоинство этого принципа состоит в точности регулирования. Регулятор, воспринимая изменение параметра j, будет реагировать лишь на отклонение j от заданного значения j0 ( ), удерживая его в определенных пределах.
), удерживая его в определенных пределах.
Недостатком этого принципа является то, что перестановка регулирующего органа будет происходить лишь по мере накопления сигнала рассогласования ±Dj, а следовательно, будет запаздывать по отношению к возмущениям l. Кроме того, сам объект регулирования может обладать большим временем запаздывания в прохождении сигнала о перемещении Р.О. под действием mрег до изменения параметра j. Система будет давать некачественный процесс регулирования.
Принцип Понсèле подразумевает регулирование по возмущению l, при этом выбирается одно или несколько основных и постоянно действующих возмущений, поддающихся измерению (рис. 1.4).
| Рис. 1.4. Структурная схема САР, работающая по принципу Понселе |
 Достоинством этого принципа является быстрота срабатывания регулятора, так как он вступает в работу сразу после изменения возмущения l, хотя параметр j еще не изменился. Недостаток – грубое регулирование, так как регулируемый параметр j не измеряется. Этот принцип как самостоятельный практически не используется.
Достоинством этого принципа является быстрота срабатывания регулятора, так как он вступает в работу сразу после изменения возмущения l, хотя параметр j еще не изменился. Недостаток – грубое регулирование, так как регулируемый параметр j не измеряется. Этот принцип как самостоятельный практически не используется.
Комбинированный принцип. Согласно этому принципу производится регулирование и по отклонению регулируемой величины и по возмущению l (рис. 1.5). Этот принцип включает в себя достоинства предыдущих и широко применяется на тепловых объектах регулирования.
| Рис. 1.5. Структурная схема САР, работающая по комбинированному принципу |
По этому признаку САР подразделяются на следующие виды: системы стабилизации, программного управления, следящие системы и оптимального (экстремального) управления.
В системах стабилизации заданное значение регулируемого параметра не изменяется с течением времени (j0=const). Система регулирования поддерживает среднее значение параметра равным заданному с допустимой погрешностью (рис. 1.6).
Стабилизирующие регуляторы получили широкое распространение при управлении технологическими системами, при регулировании какого-либо одного параметра (уровня, температуры, давления, концентрации, скорости и т.п.).
| Рис. 1.6. График работы системы стабилизации |

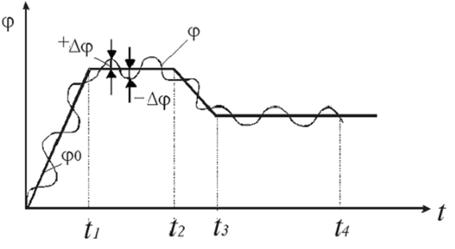
В системах программного регулирования заданное значение регулируемого параметра изменяется по определенной жестко заданной программе (j0=f(t)). Система регулирования изменяет среднее значение регулируемого параметра во времени в соответствии с программой. Примером такой системы является регулирование температуры в печи для термообработки металлических изделий (рис. 1.7). В течение времени (0¸t1) выдерживается скорость нагрева садки с металлическими изделиями; (t1¸t2) – время выдержки постоянного значения температуры для формирования структуры металла с нужным размером зерен; (t2¸t3) – охлаждение садки с нужной скоростью; (t3¸t4) – время выдержки металлических изделий для стабилизации структуры.
| Рис. 1.7. График работы программной системы регулирования |
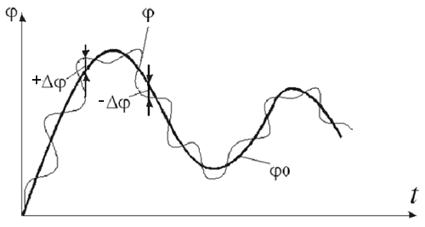
В следящих системах (системах соотношения) имеются, как правило, два параметра. Один из них изменяется во времени случайным образом, а второй должен изменяться так же или в каком-либо соотношении к нему. Изменение первого параметра является переменным заданием (j0) для регулирования второго параметра (j) – рис. 1.8. К таким системам могут быть отнесены системы регулирования соотношения «топливо – воздух» в топках котельных установок или печах нагрева. Известно, что для сжигания какого-либо количества топлива требуется определенное количество воздуха. Расход топлива (допустим, природного газа) изменяется регулятором тепловой нагрузки котла, колебания которой определяются потребителем пара (или горячей воды), или регулятором температуры в печи нагрева. Изменение расхода топлива (первый параметр) принимается за заданное значение (j0) для регулирования расхода воздуха (второй параметр j). Регулятор изменяет расход воздуха в соответствии с изменением расхода топлива (для природного газа в соотношении, например, 1:10).
| Рис. 1.8. График работы следящей системы |
Системы оптимального (экстремального) управления обеспечивают отыскание и поддержание таких регулирующих воздействий на объект регулирования при изменении нагрузок (возмущений) на него, для которых регулируемая величина имеет наибольшее (наименьшее) значение в установившихся режимах работы. В этих системах предварительно выбирается критерий оптимальности (максимальная температура в печи, максимальный коэффициент полезного действия работы агрегата при разных нагрузках, минимум затрат энергии на производство какого-либо вида продукции и т.п.).
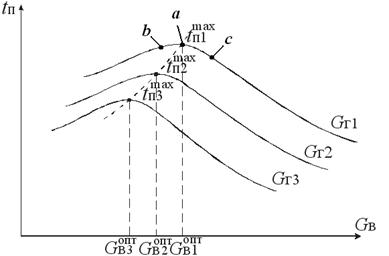
Реализация критерия оптимальности возможна только при создании достаточно сложных систем автоматического управления. Простейшим примером экстремального управления (регулирования) служит реализация критерия – поддержание максимальной температуры среды в печи при различных тепловых нагрузках, определяемых расходом газа. Максимальная температура среды будет тогда, когда расход воздуха, подаваемого на сжигание газа, будет соответствовать оптимальному для каждого расхода газа. При количестве подаваемого воздуха, меньшем необходимого, часть топлива не сгорит (химический недожог топлива), поэтому количество выделившейся при сжигании топлива теплоты будет меньше, чем можно было бы получить. При количестве воздуха, большем необходимого, часть выделившейся при сжигании топлива теплоты будет затрачена на нагрев избыточного (балластного) воздуха, т.е. и в этом случае не будет получено максимальное значение температуры дымовых газов. Влияние расхода воздуха на температуры дымовых газов в печи при разных расходах газа показано на рис. 1.8.
Рис. 1.8. Статическая характеристика печи при разных расходах газа
Gг – расход газа; Gв – расход воздуха; tп – температура дымовых газов в печи:
Точки: а –  ;
b – ;
b – 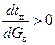 ; c – ; c – 
|
Упрощенную систему, реализующую заданный алгоритм управления, можно составить из следующих соображений.
Из статической характеристики печи следует, что оптимальный расход воздуха  , которому соответствует максимальная температура среды в печи
, которому соответствует максимальная температура среды в печи  , может быть определен по производной
, может быть определен по производной  (точка а). Если
(точка а). Если  (точка b), то воздуха подается недостаточно, а при
(точка b), то воздуха подается недостаточно, а при  (точка с) воздуха подается много. Для определения
(точка с) воздуха подается много. Для определения  в систему должны быть включены дифференциаторы, на выходе которых будет сигнал производных по времени t
в систему должны быть включены дифференциаторы, на выходе которых будет сигнал производных по времени t  , и делитель, на выходе которого получается
, и делитель, на выходе которого получается  . Схема такой системы управления представлена на рис. 1.9.
. Схема такой системы управления представлена на рис. 1.9.
| Рис. 1.9. Упрощенная схема экстремальной системы регулирования температуры в печи: ДТ – датчик температуры (термопара); ДР – датчик расхода воздуха; ДФ – дифференциатор; ДЛ – делитель; УУ – усилитель (управляющее) устройство; ИМ – исполнительный механизм; Р.О. – регулирующий орган |
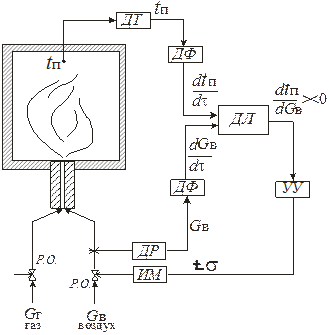
При  управляющее устройство увеличивает подачу воздуха, а при
управляющее устройство увеличивает подачу воздуха, а при  – уменьшает. При
– уменьшает. При  система отключена, подается оптимальный расход воздуха
система отключена, подается оптимальный расход воздуха  .
.
В зависимости от вида статической характеристики информационные САР подразделяются на астатические и статические.
Под статической характеристикой системы регулирования понимают зависимость регулируемого параметра j от нагрузки на объект (возмущения l) в установившихся режимах работы.
В астатических системах среднее значение регулируемого параметра j в пределах зоны нечувствительности регулятора Dнеч равно заданному значению j0 в установившихся режимах работы и не зависит от нагрузки на объект регулирования (рис. 1.10).
| Рис. 1.10. Статическая характеристика астатических систем регулирования: Dнеч – зона нечувствительности |

Под зоной нечувствительности Dнеч регулятора понимают диапазон изменений регулируемого параметра j, в пределах которого регулятор не работает (не чувствует). Зона нечувствительности определяется тем, что в элементах системы существуют силы трения, зазоры в сочленениях при механических передачах сигналов (датчик, исполнительный механизм, их соединения с регулирующими органами и т.п.) и регулирующий орган будет перемещаться не сразу, а только после отклонения регулируемого параметра на определенную величину, необходимую для преодоления сил трения и зазоров. Мы не знаем, какое значение принимает параметр в пределах зоны нечувствительности, и можем говорить только о среднем его значении. Достоинством астатических систем является точное регулирование (без статической ошибки).
В статических системах наблюдается пропорциональная связь между средним значением регулируемого параметра j и нагрузкой на объект регулирования l в установившихся режимах работы во всем диапазоне изменения нагрузок (рис. 1.11).
| Рис. 1.11. Статическая характеристика статических систем регулирования: lmin, lmax – минимальное и максимальное значения нагрузок; jmax, jmin, j0 –максимальное, минимальное и заданное значения регулируемого параметра; Djст – статическая ошибка регулирования при нагрузке на объект l |

В этих системах появится неравномерность регулирования. Разность между максимальным и минимальным установившимися значениями регулируемого параметра  называют абсолютной неравномерностью. Чаще статические системы сравниваются по относительной неравномерности, относя абсолютную неравномерность к заданному или среднему значению регулируемого параметра:
называют абсолютной неравномерностью. Чаще статические системы сравниваются по относительной неравномерности, относя абсолютную неравномерность к заданному или среднему значению регулируемого параметра:
 .
.
Статические системы обычно имеют относительную неравномерность в пределах d»4 – 8 %.
В зависимости от характера работы исполнительного механизма САР подразделяются на системы непрерывного и дискретного действия.
САР непрерывного действия имеет исполнительный механизм с переменной скоростью, и регулирующий орган непрерывно следит за изменением регулируемой величины до тех пор, пока измеренное значение регулируемой величины не будет совпадать с заданным значением (астатическая система) или не установится на новом значении (статическая система).
САР дискретного действия имеет исполнительный механизм с постоянной скоростью или реле. В регуляторах с этими типами исполнительных механизмов проходящий сигнал квантуется по уровню сигнала, по времени или по уровню и времени. В зависимости от вида квантования различают следующие системы дискретного действия: релейные, импульсные и цифровые.
Релейные системы имеют в своем составе релейный элемент, осуществляющий квантование по уровню, т.е. по величине (или мощности) отклонения параметра от заданного значения. Исполнительный механизм будет работать в течение времени, пока отклонение параметра, выйдя за пределы зоны нечувствительности и включив регулятор в работу, не вернется обратно в пределы зоны нечувствительности (регулятор отключен).
Импульсные системы имеют в своем составе импульсный элемент, преобразующий проходящий непрерывный сигнал управления в квантованный по времени. Исполнительный механизм будет включаться и работать дискретно, через равные промежутки времени с одинаковой длительностью включения (импульсами).
В цифровых системах имеется импульсный элемент и кодирующее устройство, позволяющее получить сигнал управления, квантованный по уровню и по времени. Исполнительный механизм будет включаться в работу через равные промежутки времени с одинаковой длительностью и переменной скоростью (исполнительные механизмы ИМ с переменной скоростью) или с разной длительностью (ИМ с постоянной скоростью).
По виду дифференциального уравнения САР подразделяются на линейные и нелинейные.
К линейным САР относятся системы, процессы в которых с достаточной точностью описываются линейными дифференциальными уравнениями. Нелинейные системы описываются нелинейными дифференциальными уравнениями, которые с достаточной для практических расчетов точностью не могут быть линеаризованы.
В зависимости от числа входных и выходных величин системы подразделяются на одномерные и многомерные.
В одномерных САР имеется одна входная и одна выходная величина, а в многомерных системах – две и более входных и выходных величин.
Известно, что любое движение, процессы передачи, обмена и преобразования энергии или вещества математически описываются дифференциальными уравнениями. Любое изменение САР также принято описывать дифференциальными уравнениями, которые определяют сущность происходящих процессов в системе независимо от принципов ее действия, назначения и конструкции. Решив дифференциальное уравнение элемента или системы в целом, можно найти характер изменения регулируемой величины в переходных и установившихся режимах при определенных задающих и возмущающих воздействиях на систему.
Для упрощения задачи нахождения дифференциального уравнения, описывающего работу САР в целом, систему разбивают на отдельные простейшие функциональные элементы и представляют ее в виде различного соединения элементов (звеньев) с указанием линий связей между ними. Такое графическое изображение САР называют структурной схемой (рис. 2.1).

Рис. 2.1. Структурная схема САР:
Линии со стрелками – связи между элементами; 1 – 10 – элементы САР;
хвх, хвых – входная выходная величины объектов регулирования
Для каждого элемента структурной схемы можно составить дифференциальное уравнение, определяющее зависимость изменения выходной величины от входной, рассмотрев физические процессы в нем. Так как выходная величина предыдущего элемента является входной величиной последующего элемента, то, определив дифференциальные уравнения отдельных элементов, путем последовательного исключения промежуточных переменных можно найти дифференциальное уравнение системы, определяющее характер изменения выходной (регулируемой) величины при изменении входной.
Однако такой метод нахождения дифференциального уравнения системы применим только в простых случаях. В большинстве же случаев в реальных элементах системы связь между входными и выходными величинами является нелинейной и часто задается в графической форме. При этом даже если и будет получено дифференциальное уравнение системы, то оно будет нелинейным. Аналитическое же решение нелинейных дифференциальных уравнений весьма затруднено, поэтому их линеаризуют, если это возможно.
Математический аппарат решения линейных дифференциальных уравнений хорошо разработан и широко используется в теории автоматического регулирования.
Линеаризация дифференциальных уравнений
Наиболее распространенным методом линеаризации является метод малых отклонений. В его основе лежит предположение о том, что в процессе регулирования входные и выходные величины незначительно отклоняются от установившегося значения. Если функции, входящие в дифференциальное уравнение, гладкие и имеют непрерывные производные, то линеаризация производится разложением функций в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму.
Рассмотрим этот метод линеаризации на следующем примере. Пусть элемент системы регулирования описывается в общем виде уравнением вида
 , (2.1)
, (2.1)
где  ,
, 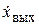 ,
,  – выходная величина элемента и ее первая и вторая производные;
– выходная величина элемента и ее первая и вторая производные;  ,
, 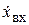 – входная величина и ее первая производная.
– входная величина и ее первая производная.
Установившийся режим имеет место при некоторых постоянных значениях величин:  ,
, 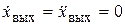 ;
; 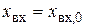 ;
;  . Тогда уравнение установившегося режима
. Тогда уравнение установившегося режима
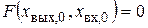 . (2.2)
. (2.2)
При изменении входной величины 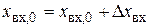 ,
,  изменится выходная величина и ее производные:
изменится выходная величина и ее производные:  ;
;  ;
;  .
.
Уравнение динамики тогда будет иметь вид
 . (2.3)
. (2.3)
Разложим эту функцию в ряд Тейлора и ограничимся только первой производной в разложении:
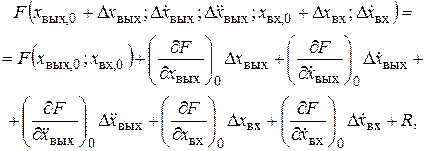 (2.4)
(2.4)
где R – остаточный член, учитывающий величины высшего порядка малости.
Вычитая из (2.4) уравнение (2.2) и пренебрегая остаточным членом R, получим линеаризованное дифференциальное уравнение в отклонениях от заданного значения:
 (2.5)
(2.5)
или
 (2.6)
(2.6)
Линеаризация статических характеристик
Статическая характеристика элемента, т.е. зависимость выходного параметра хвых,0 от входного хвх,0 в установившихся режимах, называется линейной, если описывается линейным уравнением и изображается на графике в виде прямой линии, и нелинейной, если она описывается нелинейным уравнением и изображается в виде кривой или ломаной линии.
Линеаризация нелинейных статических характеристики осуществляется несколькими способами.