Тема 14. Принятие решение в условиях риска на основе модели игры с природой
Рассмотрим игру с природой, в которой статистик-игрок А имеет т возможных стратегий  , а природа П может пребывать в одном из п своих состояний
, а природа П может пребывать в одном из п своих состояний 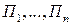 . Предположим, что статистик может оценить последствия применения каждой своей чистой стратегии
. Предположим, что статистик может оценить последствия применения каждой своей чистой стратегии  в зависимости от каждого состояния
в зависимости от каждого состояния  природы П, т. е. статистику известен численный результат
природы П, т. е. статистику известен численный результат  при выборе каждой стратегии
при выборе каждой стратегии  , и при каждом состоянии природы
, и при каждом состоянии природы  . Тогда, как мы знаем из предыдущего § 13, игру с природой можно задать платежной матрицей
. Тогда, как мы знаем из предыдущего § 13, игру с природой можно задать платежной матрицей
| А= | 

| 
| 
| … | 
|
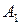
| 
| 
| … | 
| |
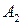
| 
| 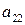
| … | 
| |
| … | … | … | … | … | |

| 
| 
| … | 
|
размера  .
.
Перед тем как переходить к выбору оптимальной стратегии, целесообразно по возможности упростить матрицу А, уменьшив число строк на основании принципа доминирования стратегий игрока А.
В понятии оптимальной стратегии лежат различные соображения, составляющие содержание соответствующих критериев оптимальности стратегий.
Критерий Байеса относительно выигрышей. Предположим, что статистику из прошлого опыта известны не только состояния 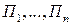 , в которых может находиться природа П, но и соответствующие вероятности
, в которых может находиться природа П, но и соответствующие вероятности , с которыми природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска.
, с которыми природа П реализует эти состояния. Тогда мы находимся в ситуации принятия решения в условиях риска.
Показателем эффективности стратегии А, по критерию Байеса относительно выигрышей называется среднее значение, или математическое ожидание выигрыша1-й строки с учетом вероятностей всех возможных состояний природы. Обозначая это среднее значение через  , будем иметь
, будем иметь
 (14.1)
(14.1)
Таким образом, представляет собой взвешенное среднее выигрышей i-й строки, взятых с весами
представляет собой взвешенное среднее выигрышей i-й строки, взятых с весами 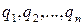 .
.
Оптимальной среди чистых стратегий по критерию Байеса относительно выигрышей считается стратегия  с максимальным показателем эффективности (14.1), т. е. с максимальным средним выигрышем
с максимальным показателем эффективности (14.1), т. е. с максимальным средним выигрышем
 . (14.2)
. (14.2)
Теорема 14.1. Стратегия  , оптимальная среди чистых стратегий по критерию Байеса относительно выигрышей, является оптимальной по тому же критерию и среди всех смешанных стратегий множества
, оптимальная среди чистых стратегий по критерию Байеса относительно выигрышей, является оптимальной по тому же критерию и среди всех смешанных стратегий множества  .
.
Теорема 14.1 показывает, что при принятии решения в условиях риска по критерию Байеса относительно выигрышей можно обойтись только чистыми стратегиями, не используя смешанные.
Пример 1. Найдем оптимальную стратегию предприятия в выпуске новых видов продукции по критерию Байеса относительно выигрышей. Платежная матрица игры


| 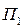
| 
| 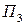
| 
|
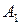
| 0,25 | 0,35 | 0?40 | 0,31 |
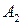
| 0,70 | 0,20 | 0,30 | 0,47 |

| 0,35 | 0,85 | 0,20 | 0,47 |
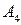
| 0,80 | 0,10 | 0,35 | 0,5 |

| 0,5 | 0,3 | 0,2 |
(14.3)
Для удобства перепишем матрицу (14.3), добавив строку вероятностей состояний природы и столбец показателей эффективности стратегий игрока А, т.е. средних выигрышей, вычисленных по формуле (14.2):
Так, например, по формуле (14.2) при 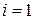
 .
.
Из последнего столбца матрицы (14.3) видно, что стратегия 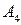 имеет наибольший показатель эффективности
имеет наибольший показатель эффективности  и, следовательно, по критерию Байеса относительно выигрышей, она является оптимальной.
и, следовательно, по критерию Байеса относительно выигрышей, она является оптимальной.
Критерий Байеса относительно рисков. Рассмотрим ту же игру с природой с матрицей (22.1), в которой известны вероятности состояний природы  . При принятии решений в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы игры, используя формулу рисков (13.2):
. При принятии решений в условиях риска можно пользоваться не только средними выигрышами, но и средними рисками. Составим матрицу рисков для матрицы игры, используя формулу рисков (13.2):


| 
| 
| … | 
|
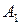
| 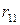
| 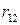
| … | 
|
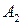
| 
| 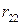
| … | 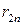
|
| … | … | … | … | … |

| 
| 
| … | 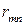
|
(14.4)
Показателем неэффективности стратегии  по критерию Байеса относительно рисков называется среднее значение (математическое ожидание) рисков
по критерию Байеса относительно рисков называется среднее значение (математическое ожидание) рисков  -й строки матрицы (22.9), вероятности которых, очевидно, совпадают с вероятностями состояний природы. Обозначим средний риск при стратегии
-й строки матрицы (22.9), вероятности которых, очевидно, совпадают с вероятностями состояний природы. Обозначим средний риск при стратегии  через
через  , тогда
, тогда
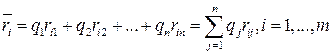 (14.5)
(14.5)
является взвешенным средним рисков  -й строки матрицы (14.4) с весами
-й строки матрицы (14.4) с весами  .
.
Оптимальной среди чистых стратегий по критерию Байеса относительно рисков является стратегия  , показатель неэффективности (14.5) которой минимален, т.е. минимален средний риск
, показатель неэффективности (14.5) которой минимален, т.е. минимален средний риск
 . (14.6)
. (14.6)
Теорема 14.1. Если  - стратегия, оптимальная среди чистых стратегий по критерию Байеса относительно рисков, то она является оптимальной по тому же критерию и среди всех смешанных стратегий множества
- стратегия, оптимальная среди чистых стратегий по критерию Байеса относительно рисков, то она является оптимальной по тому же критерию и среди всех смешанных стратегий множества  .
.
Критерий Лапласа относительно выигрышей. В предыдущих двух критериях Байеса известные вероятности  состояний природы могли быть получены из статистических данных, отражающих многократное решение подобных задач, или в результате наблюдений за поведением природы. Однако довольно часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояний природы указанными способами. Желая все же принять решение в условиях риска, мы вынуждены оценить вероятности состояний природы субъективно. Существуют различные методы численной субъективной оценки степени правдоподобности состояний природы. Один из них состоит в том, что мы не можем отдать предпочтение ни одному из состояний природы и потому считаем их равновероятными, т.е.
состояний природы могли быть получены из статистических данных, отражающих многократное решение подобных задач, или в результате наблюдений за поведением природы. Однако довольно часто складывается такая ситуация, когда мы лишены возможности определить вероятности состояний природы указанными способами. Желая все же принять решение в условиях риска, мы вынуждены оценить вероятности состояний природы субъективно. Существуют различные методы численной субъективной оценки степени правдоподобности состояний природы. Один из них состоит в том, что мы не можем отдать предпочтение ни одному из состояний природы и потому считаем их равновероятными, т.е.  . Этот принцип называется "принципом недостаточного основания " Лапласа. На нем основан критерий Лапласа относительно выигрышей.
. Этот принцип называется "принципом недостаточного основания " Лапласа. На нем основан критерий Лапласа относительно выигрышей.
Показателем эффективности стратегии  по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей
по критерию Лапласа относительно выигрышей называется среднее арифметическое выигрышей  -й строки:
-й строки:
 . (14.7)
. (14.7)
Оптимальной среди чистых стратегий по критерию Лапласа относительно выигрышей считается стратегия  ,показатель эффективности которой, вычисляемый по формуле (14.7), максимален, т е.
,показатель эффективности которой, вычисляемый по формуле (14.7), максимален, т е.  .
.
Пример. Рассмотрим игру с природой, заданную матрицей игры


| 
| 
| 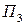
| 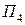
|
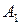
| 2 | |||
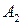
| ||||

| ||||
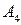
|
Вероятности состояний природы неизвестны. Будем считать, что все четыре возможные состояния природы равновероятны. Найдем оптимальную стратегию по критерию Лапласа относительно выигрышей. Перепишем матрицу выигрышей, добавив столбец показателей эффективности стратегий, вычисляемых по формуле (14.7) без множителя  в правой части:
в правой части:


| 
| 
| 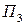
| 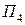
| 
|
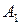
| 2 | ||||
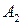
| |||||

| |||||
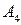
|
(14.8)
Так, например,  . Из последнего столбца матрицы (14.8) видно, что наибольшим показателем эффективности обладает стратегия А3, для которой а3= 26.
. Из последнего столбца матрицы (14.8) видно, что наибольшим показателем эффективности обладает стратегия А3, для которой а3= 26.
Значит, по критерию Лапласа относительно выигрышей оптимальной является стратегия  .
.
Критерий Лапласа относительно рисков. Критерий Байеса относительно рисков при равновероятных состояниях природы,  , превращается в критерий Лапласа относительно рисков. Тогда величина
, превращается в критерий Лапласа относительно рисков. Тогда величина  или более простая величина представляет собой показатель неэффективности стратегии
или более простая величина представляет собой показатель неэффективности стратегии  по критерию Лапласа относительно рисков. Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия
по критерию Лапласа относительно рисков. Следовательно, оптимальной среди чистых стратегий по критерию Лапласа относительно рисков является стратегия  , показатель неэффективности
, показатель неэффективности 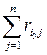 которой минимален. Подставляя в (14.5) значения
которой минимален. Подставляя в (14.5) значения  , получим показатель неэффективности смешанной стратегии Р по критерию Лапласа относительно рисков, вместо которого можно рассматривать более простую величину
, получим показатель неэффективности смешанной стратегии Р по критерию Лапласа относительно рисков, вместо которого можно рассматривать более простую величину 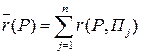 . Стратегия Р, для которой показатель
. Стратегия Р, для которой показатель  принимает минимальное значение, является оптимальной среди всех стратегий множества
принимает минимальное значение, является оптимальной среди всех стратегий множества  .
.
Критерий относительных значений вероятностей состояний природы с учетом выигрышей. В практике принятия решений часто встречается случай, когда нам неизвестны вероятности состояний природы, но мы имеем представление о том, какие состояния природы более правдоподобны, какие - менее правдоподобны, а какие — равноправдоподобны. Поэтому мы можем расположить (неизвестные) вероятности состояний природы в виде убывающей или возрастающей последовательности. Для простоты предположим, что расположение  уже и есть монотонная последовательность. Если, например, эта последовательность строго убывает, то правдоподобнее всех состояние
уже и есть монотонная последовательность. Если, например, эта последовательность строго убывает, то правдоподобнее всех состояние  , затем по степени правдоподобности следует состояние
, затем по степени правдоподобности следует состояние  , и т.д., наименьшей правдоподобностью обладает состояние
, и т.д., наименьшей правдоподобностью обладает состояние  . Не зная, на сколько одна вероятность состояния природы отличается от другой, мы можем предположительно придать им относительные значения, пропорциональные членам некоторой (подходящей на наш взгляд) монотонной последовательности положительных чисел
. Не зная, на сколько одна вероятность состояния природы отличается от другой, мы можем предположительно придать им относительные значения, пропорциональные членам некоторой (подходящей на наш взгляд) монотонной последовательности положительных чисел  , т.е.
, т.е.
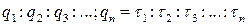 . (14.9)
. (14.9)
Из (14.9) следует, что если  - убывающая, соответственно возрастающая, последовательность, то убывающей, соответственно возрастающей, является и последовательность
- убывающая, соответственно возрастающая, последовательность, то убывающей, соответственно возрастающей, является и последовательность  . В самом деле, если
. В самом деле, если  - убывающая последовательность, т. е.
- убывающая последовательность, т. е. 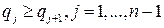 , то
, то  . Тогда из (14.9)
. Тогда из (14.9)  , откуда ,
, откуда ,  , что и означает убывание последовательности
, что и означает убывание последовательности  . Если
. Если  возрастающая последовательность, то возрастание последовательности
возрастающая последовательность, то возрастание последовательности  доказывается аналогично.
доказывается аналогично.
Из (14.9) и нормировочного равенства
 (14.10)
(14.10)
можно выразить вероятности  через числа
через числа  .
.
Действительно, из (14.9) , откуда
, откуда
 . (14.11)
. (14.11)
Из (14.9)  , откуда
, откуда 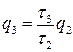 , или после подстановки сюда равенства (14.11)
, или после подстановки сюда равенства (14.11)

и т.д.
 . (14.12)
. (14.12)
Следовательно, из (22.30)
 . (14.131)
. (14.131)
Итак, исходя из наших предположений, мы нашли значения вероятностей  состояний природы.
состояний природы.
В частности, если  - арифметическая профессия с положительными членами и разностью
- арифметическая профессия с положительными членами и разностью 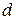 , то
, то
 . (14.14)
. (14.14)
Если  - геометрическая прогрессия с положительными членами и (следовательно, с положительным) знаменателем
- геометрическая прогрессия с положительными членами и (следовательно, с положительным) знаменателем 
 .
.