Тема 9. Принцип доминирования
Отыскать решения игр без седловой точки, особенно при достаточно больших размерах платежной матрицы, оказывается довольно сложной задачей. В некоторых случаях эту задачу можно упростить с помощью редуцирования игр, т. е. сведения данной игры со сложной матрицей к игре с более простой матрицей. В этом параграфе мы рассмотрим один из способов редуцирования игр, основанный на принципе доминирования, который позволяет в некоторых случаях игру с матрицей большего размера свести к игре с матрицей меньшего размера.
Пусть имеем игру с матрицей 
| А= |  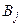 Ai
Ai
| 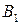
| 
| … | 
|
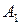
| 
| 
| … | 
| |
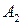
| 
| 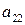
| … | 
| |
| … | … | … | … | … | |

| 
| 
| ... | 
|
Каждой смешанной (в частности, чистой) стратегии  игрока А поставим в соответствие строку
игрока А поставим в соответствие строку
 (9.1)
(9.1)
Строку (9.1) можно представить так:
 (9.2)
(9.2)
Обратно, каждой выпуклой комбинации (9.2) строк матрицы А с коэффициентами  поставим в соответствие смешанную стратегию
поставим в соответствие смешанную стратегию  игрока А.
игрока А.
Таким образом, между смешанными (в том числе и чистыми) стратегиями  игрока А и выпуклыми комбинациями
игрока А и выпуклыми комбинациями

строк матрицы А устанавливается взаимно-однозначное соответствие
матрицы А устанавливается взаимно-однозначное соответствие
 (9.3)
(9.3)
Из (9.1) или (9.3) ясно, что каждой чистой стратегии  игрока А ставится во взаимно-однозначное соответствие k-я строка
игрока А ставится во взаимно-однозначное соответствие k-я строка  матрицы А.
матрицы А.
Если для двух выпуклых комбинаций строк матрицы А
 (9.4)
(9.4)
 (9.5)
(9.5)
выполняются неравенства
 , (9.6)
, (9.6)
то говорят, что строка (9.5) доминирует строку (9.4), а строка (9.4) доминируется строкой (9.5). Таким образом, строка(11.5) — доминирующаястроку (9.4), а строка (9.4) — доминируемая строкой (9.5).
Если каждое из неравенств (9.6) является равенством, то строки (9.4) и (9.5) называют дублирующими друг друга. Каждая из двух дублирующих строк является одновременно и доминируемой, и доминирующей другую.
Если каждое из неравенств (9.6) является строгим, то говорят, что строка (9.5) строго доминирует строку (9.4), а строка (9.4) строго доминируется строкой (9.5), или строка (9.5) является строго доминирующей строку (9.4), а строка (9.4) является строго доминируемой строкой (9.5).
Аналогичная терминология используется и для соответствующих стратегий игрока А. А именно, если строка (9.5) доминирует, соответственно дублирует, соответственно строго доминирует строку (9.4), то говорят, что стратегия  доминирует, соответственно дублирует, соответственно строго доминирует стратегию
доминирует, соответственно дублирует, соответственно строго доминирует стратегию  .
.
Так как элементами строк, соответствующих по (9.3) смешанным стратегиям, являются выигрыши игрока А (см. (9.1)), то из данных определений понятно, что для игрока А дублирующие стратегии равнопредпочтительны, а доминируемая не дублирующая стратегия заведомо для него невыгодна.
Аналогично, каждой смешанной (в частности, чистой) стратегии  игрока В поставим в соответствие столбец
игрока В поставим в соответствие столбец
 (9.7)
(9.7)
Если для двух выпуклых комбинаций столбцов матрицы А
 ,
,  (9.8)
(9.8)

 (9.9)
(9.9)
справедливы неравенства
 ,
,  ,...,
,..., , (9.10)
, (9.10)
то говорят, что столбец (9.8) (стратегия  ) доминирует столбец (9.9) (стратегию
) доминирует столбец (9.9) (стратегию ) а столбец (9.9) (стратегия
) а столбец (9.9) (стратегия  ) доминируется столбцом (9.8) (стратегией
) доминируется столбцом (9.8) (стратегией  ).
).
В случае, когда каждое неравенство (9.10) является равенством, столбцы (9.8) и (9.9) (стратегии  и
и  ) называются дублирующими.
) называются дублирующими.
Если каждое неравенство (9.10) является строгим, то столбец (9.8) (стратегия ) называется строго доминирующим (строго доминирующей) столбец (9.9) (стратегию
) называется строго доминирующим (строго доминирующей) столбец (9.9) (стратегию ), а столбец (11.11) (стратегия
), а столбец (11.11) (стратегия ) - строго доминируемым (строго доминируемой) столбцом (11.10) (стратегией
) - строго доминируемым (строго доминируемой) столбцом (11.10) (стратегией ).
).
Теорема 9.1. Справедливы следующие предложения.
1 .Если  -я строка,
-я строка,  , матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее строк, то существует оптимальная смешанная стратегия
, матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее строк, то существует оптимальная смешанная стратегия  игрока А, в которой
игрока А, в которой  -я чистая стратегия
-я чистая стратегия  выбирается им с нулевой вероятностью, т.е
выбирается им с нулевой вероятностью, т.е .
.
2. Если  -я строка,
-я строка,  , матрицы
, матрицы  игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то в любой оптимальной смешанной стратегии
игры строго доминируется некоторой выпуклой комбинацией остальных ее строк, то в любой оптимальной смешанной стратегии  игрока А чистая
игрока А чистая  -я стратегия
-я стратегия  выбирается им с нулевой вероятностью, т.е.
выбирается им с нулевой вероятностью, т.е. .
.
3. Если  -й столбец,
-й столбец, , матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее столбцов, то существует оптимальная смешанная стратегия
, матрицы А игры доминируется некоторой выпуклой комбинацией остальных ее столбцов, то существует оптимальная смешанная стратегия  игрока В, в которой
игрока В, в которой  -я чистая стратегия
-я чистая стратегия  выбирается им с нулевой вероятностью, т.е.
выбирается им с нулевой вероятностью, т.е.  .
.
4. Если  -й столбец,
-й столбец,  , матрицы А игры строго доминируется некоторой выпуклой комбинацией остальных ее столбцов, то в любой оптимальной смешанной стратегии
, матрицы А игры строго доминируется некоторой выпуклой комбинацией остальных ее столбцов, то в любой оптимальной смешанной стратегии  игрока В чистая
игрока В чистая  -я стратегия
-я стратегия  выбирается им с нулевой вероятностью, т е.
выбирается им с нулевой вероятностью, т е. .
.
Следствие 9.1.
1. Если  -я строка матрицы игры доминируется (строго доминируется) некоторой другой строкой, то существует (любая) оптимальная смешанная стратегия игрока А, в которую чистая стратегия
-я строка матрицы игры доминируется (строго доминируется) некоторой другой строкой, то существует (любая) оптимальная смешанная стратегия игрока А, в которую чистая стратегия  входит с нулевой вероятностью.
входит с нулевой вероятностью.
2. Если  -й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия
-й столбец матрицы игры доминируется (строго доминируется) некоторым другим столбцом, то существует (любая) оптимальная смешанная стратегия игрока В, в которую чистая стратегия  входит с нулевой вероятностью.
входит с нулевой вероятностью.
Следствие 9.2 (о дублирующих чистых стратегиях). Одну из двух дублирующих чистых стратегий можно удалить.
Пример 11.1. Рассмотрим игру 3x5 с матрицей


| 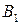
| 
| 
| 
| 
| (9.11) |
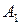
| -2 | |||||
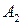
| -1 | -4 | -1 | -4 | ||

| -5 | -5 |
В данной матрице и
и  - дублирующие стратегии игрока В. Поэтому в соответствии со следствием 9.2 один из этих столбцов можно удалить. Удалим, например, 5-й столбец. В оставшейся матрице 3-й Столбец строго, а 4-й столбец нестрого доминируются 1-м столбцом. Поэтому можно удалить также 3-й и 4-й столбцы. В результате получим матрицу
- дублирующие стратегии игрока В. Поэтому в соответствии со следствием 9.2 один из этих столбцов можно удалить. Удалим, например, 5-й столбец. В оставшейся матрице 3-й Столбец строго, а 4-й столбец нестрого доминируются 1-м столбцом. Поэтому можно удалить также 3-й и 4-й столбцы. В результате получим матрицу


| 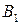
| 
| (9.12) |
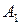
| -2 | ||
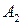
| -1 | -4 | |

| -5 |
2-я строка матрицы (9.12) строго доминируется выпуклой комбинацией 1-й и 3-й строк с коэффициентами и
и  :
:

Поэтому нужно отбросить 2-ю строку. В результате получим матрицу
 
| 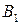
| 
| (9.13) |
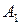
| -2 | ||
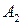
| -5 |
Нижняя цена в чистых стратегиях игры с матрицей (11.25)  , а верхняя цена
, а верхняя цена  . Так как
. Так как  , то решение надо искать в смешанных стратегиях. Предположим, что
, то решение надо искать в смешанных стратегиях. Предположим, что  и
и  - оптимальные стратегии игроков и V - цена игры с матрицей (9.13). Тогда по необходимым условиям оптимальности стратегий, сформулированным в теореме 9.2, имеем:
- оптимальные стратегии игроков и V - цена игры с матрицей (9.13). Тогда по необходимым условиям оптимальности стратегий, сформулированным в теореме 9.2, имеем:
 (9.14)
(9.14)
Умножив 1-е неравенство системы (9.14) на 2 и прибавив ко 2-му, получим
 (9.15)
(9.15)
Умножив 3-е неравенство системы (9.4) на 2 и прибавив к 4-му, получим
 (9.16)
(9.16)
Из неравенств (9.15) и (9.16) следует равенство  . Подставим найденное значение V в систему (9.15):
. Подставим найденное значение V в систему (9.15):
 (11.29)
(11.29)
Из первых двух уравнений системы (11.29):  , а из вторых двух уравнений:
, а из вторых двух уравнений: .
.
Учитывая удаленные столбцы и строку для исходной игры с матрицей (11.11), получим следующее (частное) решение:
 .
.
Поскольку 4-й столбец матрицы (11.23) нестрого доминировался 1-м столбцом, то могут существовать и другие оптимальные стратегии игрока В, в которых чистая стратегия 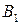 будет входить с положительной вероятностью.
будет входить с положительной вероятностью.