Максиминные и минимаксные стратегии. Нижняя и верхняя цены игры в чистых стратегия

Тема 3. Антагонистические игры

Рассмотрим матричную - игру с игроками А и В, в которой игрок А обладает чистыми стратегиями , а игрок В - чистыми стратегиями . Значения функции выигрыша игрока А обозначим через , т. е. .

Поскольку всевозможные действия игроков в матричной игре описываются множеством возможных стратегий, то задача состоит в выборе такой стратегии, которая способствует достижению поставленной цели - максимизации выигрыша для игрока А или минимизации проигрыша для игрока В. Итак, перед игроком А стоит задача выбора чистой стратегии из множества , эффективной в определенном смысле, в результате применения которой он получит максимально возможный гарантированный выигрыш. Если игрок А выбрал стратегию , то его выигрышем может быть один из выигрышей

, (3.1)

расположенных в –й строке матрицы (3.1), в зависимости от выбранной игроком В стратегии. Предполагая поведение игрока А крайне осмотрительным, необходимо считать, что игрок В сыграет наилучшим для себя образом и на выбор игроком А стратегии выберет ту стратегию , при которой выигрыш игрока А окажется минимальным. Обозначим минимальный среди выигрышей (5.1) через :

(3.2)

и назовем его показателем эффективности стратегии А,. Продолжая действовать разумно, игрок А должен выбрать ту стратегию, которая максимизирует показатель эффективности, т.е. для которой число максимально. Если обозначить это максимальное число через

, (3.3)

то по формуле (5.2)

. (3.4)

Описанный принцип (3.3) или (3.4) выбора эффективной стратегии игроком А называется макашштым принципом, а выигрыш - максимином. Стратегия , соответствующая максимину , называется максминной стратегией игрока А. Множество всех (чистых) максиминных стратегий игрока А обозначим через .

Аналогично вводится критерий оценки выигрышей для игрока В. Как игрок В предполагает, что игрок А играет наилучшим для себя образом, то выигрышем игрока А будет максимальное из чисел (5.7); обозначим его через :

(3.5)

и назовем показателем неэффективности стратегии . Таким образом, для любой стратегии игрока В наибольший его проигрыш равен. В интересах игрока В - выбрать стратегию с минимальным показателем неэффективности. Наименьшее из чисел (3.5) обозначим :

(5.9)

Отсюда в силу формулы (3.5) получим для выражение:

(3.6)

Выбор игроком В стратегии с наименьшим показателем оправдывает то, что он назван показателем неэффективности.

Критерий (3.6) выбора эффективной стратегии для игрока В называется минимаксным принципом, а выигрыш называется минимаксом. Стратегия , для которой

(3.7)

называется минимаксной стратегией игрока В. Множество всех (чистых) минимаксных стратегий игрока В обозначим через

Величину называют верхней ценой игры.

Для нахождения нижней и верхней цен игры удобно матрицу игры (4.1) увеличить в размерах, приписав -й столбец показателей эффективности стратегий игрока А и -ю строку показателей неэффективности , стратегий игрока В, В результате получим следующую матрицу:

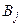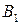
А=	Ai			…			(3.8)
			…
			…
…	…	…	…	…	…
			...
				…

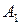
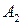
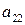
Теорема 5.1. Для элементов матрицы (3.8) имеют место неравенства

и, следовательно, нижняя цена игры не больше ее верхней цены в чистых стратегиях:

(3.9)

Пример 5.1. Найти нижнюю и верхнюю цены игры, а также макси- минные стратегии игрока А и минимаксные стратегии игрока В в условиях примера 4.2 при денежным единицам.

Решение. Определяя показатели эффективности стратегий и неэффективности стратегий , мы из матрицы (4.2) получим матрицу

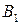
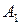
	-3			-3
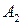
		-2		-2
			-2	-2
				-2

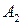из которой видно, что нижняя цена игры , а верхняя цена игры. Так как , то стратегии и игрока А являются максиминными: . Аналогично, из равенств вытекает, что каждая из стратегий игрокаВ является минимаксной: .