Основные понятия
Многие социально-экономические ситуации (особенно при рыночной экономике), в которых рассматривается вопрос о выборе решения, обладают тем свойством, что в них сталкиваются не менее двух сторон с различными (иногда противоположными) интересами, каждая из которых для достижения своей цели имеет возможность действовать различными способами, выбор которых при некоторых условиях может осуществляться в зависимости от действий противоборствующей стороны. Такие ситуации называются конфликтными. Конфликтная ситуация характеризуется следующими чертами:
1) наличие заинтересованных сторон (в качестве которых могут выступать потребители, фирмы, отдельные страны, различные таможенные, торговые, финансовые и экономические союзы, индивидуумы и т.д.)
2) существование возможных действий каждой из сторон (выбор объема потребления, выбор дивидендной политики, различные способы комплектования инвестиционного портфеля, выбор объемов выпуска, недопущение на национальный рынок некоторых товаров по политическим или экономическим соображениям, заключение договоров о представлении «режима наибольшего благоприятствования» и т.д.).
3) интересы сторон (удовлетворение различных политических, финансовых, экономических потребностей, монопольные прибыли, вытеснение конкурентов с рынка сбыта, распродажа избыточного товара на внешнем рынке, повышение доходов казны и производителей и т.д.)
Выбор поведения каждой из сторон в реальных жизненных конфликтах – сложная задача. Поэтому для ее анализа прибегают к математическому моделированию, отбрасывая несущественные факторы данной конфликтной ситуации и ограничивая ее протекание определенными правилами.
Математическая модель конфликтной ситуации называется игрой. Раздел теории исследования операций, занимающийся математическими моделями принятия оптимальных решений в условиях конфликта, называется теорией игр.
Математико-игровые модели находят свое применение не только в конфликтных ситуациях социально-экономической области, но и во взаимодействии человека с природой, в политике, в биологии, в военной области и др.
Заинтересованные стороны (в частности, лица) в игре называются игроками. Часто, хотя и не всегда, все игроки читаются равноправными. В некоторых играх по различным причинам создаются объединения. Так, если целью объединения являются совместные действия, то эти объединения называются коалициями действия. Если же объединение образовано по признаку идентичности предпочтений исходов игры, то они называются коалициями интересов. Указанные коалиции не всегда совпадают. В случае совпадения их называют просто коалициями. С точки зрения временного фактора коалиции могут быть временные или постоянные на протяжении игры. Если в игре участвуют два противника, то она называется парной. Если число противников более двух, то игра называется множественной. Множественная игра с двумя постоянными коалициями есть не что иное, как парная игра.
С целью математической формализации игра, как было отмечено выше, должна проходить по определенным правилам, представляющим собой систему условий, описывающих:
· возможные действия каждого из игроков;
· объем информации, которую может получить каждая сторона о действиях другой;
· исход игры в результате каждой совокупности ходов противников.
Любое возможное в игре действие игрока называется его стратегией или, точнее, чистой стратегией (в отличие от понятия смешанной стратегии, которое будет рассмотрено нами позже в § 7).
Игра называется конечной, если множество стратегий каждого игрока конечно. В противном случае (т.е. когда множество стратегий хотя бы одного игрока бесконечно), игра называется бесконечной. В дальнейшем будем рассматривать только конечные игры.
Говорят, что ситуация х предпочтительнее (для данного игрока) ситуации у, и пишут , если
, если  , но не
, но не  . Ситуации х и у равнопредпочтительны: х~у, если
. Ситуации х и у равнопредпочтительны: х~у, если и
и ; и, наконец, ситуации несравнимы по предпочтению, если не выполняется ни одно из соотношений
; и, наконец, ситуации несравнимы по предпочтению, если не выполняется ни одно из соотношений и
и  .
.
Чаще, однако, степень удовлетворения интересов игрока А характеризуется его функцией выигрыша , определенной на множестве
, определенной на множестве  всех ситуаций и ставящей в соответствие каждой ситуации
всех ситуаций и ставящей в соответствие каждой ситуации  некоторое число
некоторое число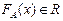 , называемое выигрышем игрока А в ситуации х. В этом случае несравнимых ситуаций уже не будет.
, называемое выигрышем игрока А в ситуации х. В этом случае несравнимых ситуаций уже не будет.
Аналогично, для игрока В функция выигрыша  определена на множестве
определена на множестве 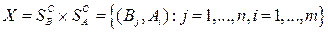 ситуаций
ситуаций  и каждой из них ставит в соответствие число
и каждой из них ставит в соответствие число , называемое выигрышем игрока В в ситуации y.
, называемое выигрышем игрока В в ситуации y.
Итак, протекание конфликтной игры состоит в выборе каждым игроком своей стратегии и получении в сложившейся ситуации выигрыша. Поэтому всякая конфликтная игра полностью описывается совокупностью, состоящей из множества игроков, множеств их возможных стратегий и множества их функций выигрыша.
Основной целью теории игр является выработка рекомендаций для удовлетворительного поведения игроков в конфликте, т. е. выявление для каждого из них "оптимальной стратегии".
Понятие оптимальной стратегии - одно из важнейших понятий теории игр. Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или эквивалентно минимально возможный средний проигрыш). Выбор оптимальной стратегии базируется на принципе, предполагающем, что оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его цели. Таким образом, теория игр абстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам в реальных случаях.
В заключение этого параграфа обратим внимание на то, что оптимальность стратегии может пониматься в различных смыслах в зависимости от показателя оптимальности (эффективности). Стратегия, оптимальная по одному показателю, совсем не обязана быть оптимальной по другому. Поэтому чаще всего оптимальная стратегия, определенная в результате применения теории игр к реальным конфликтным ситуациям, является теоретически оптимальной и в большинстве случаев реально удовлетворительной.