Добавление к § 5.2. Модель Курно, как биматричная (и n-персонная) игра.

ТЕОРИЯ АНАЛИЗА ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ

Курс лекций

Редактор Ж. А. Коваленко

Технический редактор В. А. Пожарицкая

Корректор Е. М. Богачева

Компьютерная верстка Н. С.Васильева

Подписано к печати __.___.2011. Формат 60х84 1/16. Гарнитура «Таймс». Усл.печ. листов ___. Уч.-изд. листов ____. Тираж ____экз. Заказ № _____.

Учреждение образования «Витебский государственный технологический университет» 210035, г. Витебск, Московский пр., 72.

Отпечатано на ризографе учреждения образования ”Витебский государственный технологический университет”.

Лицензия № 02330/0494384 от 16 марта 2009 г.

Курс лекций

2.Основные результаты классической модели.Модель Курно началась с его работы [1] 1838 г. Она посвящена олигополии. Олигополия- один из распространенных типов рыночной структуры. На олигопольном рынке несколько фирм конкурируют друг с другом, и вступление на этот рынок других фирм затруднено. Простейшим случаем олигополии является дуополия- рынок, на котором два производителя поставляют один и тот же товар.

Итак, рассмотрим две фирмы , выпускающие один и тот же товар. Пусть полные затраты -й фирмы при выпуске равны (таким образом, есть себестоимость выпуска одной единицы товара). В этом кратком начальном описании модели Курно полные затраты не конкретизируются: на производственные, затраты на покупку ресурсов, выплату заработной платы, затраты на обучение и переподготовку персонала т.д. Произведенный обеими фирмами товар поступает на общий рынок. Цена на товар на этом рынке линейно падает в зависимости от поступающего на рынок общего его количества , т.е. . Такое поведение цены обеспечивает полную распродажу всего поступившего на рынок товара. Следовательно, прибыль -й фирмы за цикл (выручка минус полные затраты) , где . Поведение каждой фирмы определяется ее стремлением максимизировать свою прибыль.

Для упрощения будем далее полагать, что , и длительность цикла равна единице времени что значительно упрощает выкладки, не меняя сути дела. Производство работает циклами, и эти циклы у обеих фирм совпадают. Параметр можно считать размером рынка, так как суммарный выпуск фирм должен быть меньше , иначе прибыль будет неположительной. Величина , играющая важную роль в образовании цены товара будет иметь важное значение в дальнейшем, поэтому ее важно назвать специально «свободный остаток рынка».

Из этого соглашения вытекает, что фирмы стремятся максимизировать свою прибыль, получаемую за цикл или, что тоже самое, за единицу времени.

Дуополия Курно может быть сведена к биматричной игре следующим образом: В предстоящем цикле первый выбирает выпуск , второй- . Их выигрыши понятны: первый выигрывает прибыль , второй- прибыль Приведем некоторые понятия и термины из теории матричных и биматричных игр:

Пара стратегий доминирует пару если и и хотя бы одно из этих неравенств строгое (чтобы исключить доминирование пары стратегий самой себя). Например пара (15,25) доминирует пару (12, 28), ибо прибыли фирм таковы (600,1000) и (114,228). Вот первый вопрос : что представляет собой множество Парето, т.е. множество недоминируемых пар стратегий? Есть ли хотя бы одна такая стратегия?

Поясним, что пара стратегий называется недоминируемой или оптимальной по Парето, если при попытке увеличить прибыль одной фирмы, прибыль другой обязательно уменьшится. Это понятие является одним из основных в теории биматричных игр и подлежит обязательному исследованию при развитии теории. При исследовании дуополии Курно понятие доминирования, пришедшее из теории игр , является весьма интересным и вызвало несколько интересных утверждений, доказательства которых опираются на хорошо развитую исследованную теорию дуополии Курно.

Теорема 1. Для пары стратегий есть доминирующая пара.

Изменим выпуски фирм, чтобы увеличить их прибыли : положим . Ясно, что. Докажем, что пара доминирует пару : или . Поскольку можно считать, что , имеем верное неравенство ибо , так как . Обращая эквивалентные преобразования, заключаем, что начальное неравенство верное, а так как аналогично окончательно заключаем, что пара доминирует пару .

Теорема 2. Множество оптимальности Парето есть . Докажем, что любая пара стратегий недоминируема. Предположим противное и пусть -доминирующая пара. Если , то пропускаем эту фразу и переходим к следующей. Иначе, воспользуемся теоремой 1 и найдем для пары доминирующую пару . Будем считать, что уже пара такова. Так как , а величины в скобках равны, то , значит, (так как . А так как и , то - противоречие с доминируемостью пары парой .

Вместе с теоремой 1 получаем окончательное доказательство теоремы 2.

Теоремы 1,2 обобщаются на произвольное число фирм . Нужно только пояснить, что значит доминирование в этом случае. Пусть -стратегии фирм, а - другой набор стратегий. Говорят, что набор доминирует набор если для каждого и хотя бы одно из этих неравенств является строгим. Дополнительно скажем, что набор стратегий является недоминируемым, когда для любого набора стратегий если из неравенств хотя бы одно неравенство не верно. Доказательство проведем для 3-х фирм. Их выпуски обозначим .

Теорема 1’. Для тройки стратегий есть доминирующая тройка.

Применим прием, уже опробованный нами ранее- изменим выпуски фирм, чтобы увеличить их прибыли: положим . Ясно, что . Докажем, что тройка доминирует тройку : поскольку можно считать, что , получаем верное неравенство . Обращая эквивалентные преобразования, заключаем, что начальное неравенство верное, а так как аналогично окончательно заключаем, что тройка доминирует тройку .

Вместе с теоремой 1’ получаем окончательное доказательство теоремы 2’.

В заключение Главы 3 остановимся на нахождении равновесия в смысле Нэша в модели Курно при описании дуополии Курно как биматричной игры. Напомним, что пара стратегий образует равновесие в смысле Нэша, если при отходе любого из участников дуополии он начнет получать меньшую прибыль, если другой участник будет продолжать придерживаться равновесной стратегии. Известна теорема Нэша о том, что в конечной биматричной игре есть хотя бы одна ситуация равновесия в смысле Нэша –доказательство теоремы см. в [2]. Докажем, что пара есть равновесная пара. В точке равновесия 1-й участник получает прибыль , если 2-й участник продолжает придерживаться равновесной стратегии. Но если 1-й участник отойдет от своей равновесной стратегии , то его прибыль уменьшится, ибо квадратичная функция имеет при максимум. Это доказательство столь просто, что непонятно, почему его столь долго искали-совсем недавно в одной из интернетовских публикаций говорилось об этом как о нерешенной проблеме.

Цитированная литература.

1. A.Соurnot Recherches sur les Principes Mathematiques de la Theorie des Richesses. Paris: Hachelette,183

2. Оуэн Г. Теория игр.-М.:Мир,1971

§5.3. ВЕКТОР ШЕПЛИ, ТЕОРЕМА ШЕПЛИ

1.Вектор Шепли;2. Вектор Шепли в простом голосовании и в квалифицированном; 3.Теорема Шепли;.

Вопросы и задачи.

Сила, значение того или иного члена группы во многом определяется его "связями", другими словами, возможностью входить в те или иные коалиции. Какие коалиции могут образоваться и почему? Как формализовать эти в высшей степени неформальные понятия? Частично это делается в данном параграфе. Так, выше было уже определено, что кооперативная игра называется простой, если =1 или 0 для любой коалиции . Такие важные вопросы, как обладание контрольным пакетом акций или процедуры голосования подпадают под это определение. Анализу таких игр далее уделено основное внимание.

1. Вектор Шепли. Рассмотрим некоторый класс кооперативных игр, например, борьбу акционеров за обладание контрольным пакетом и голосующих своими акциями - как в Примере 2 из п.2.2 . Возможна ли некоорая общая процедура, позволяющая определить силу каждого акционера, учитывая, с одной стороны, число акций, которыми он обладает, и с другой, его возможности войти в коалицию, которая имеет контрольный пакет? В какой-то мере на этот вопрос отвечает вектор Шепли. Этот вектор вводится аксиоматически, но, конечно, аксиомы отражают некоторые интуитивно обоснованные требования.

Рассмотрим какую-нибудь кооперативную игру с характеристической функцией .

Определение. Коалиция T называется носителем если для любой коалиции .

Тем самым, любой член группы, не входящий в коалицию не играет никакой роли: он не может внести ничего ни в какую коалицию и потому сам ничего не может получить от вхождения в ту или иную коалицию. Таких членов группы называют "болванами".

Данная группа может участвовать в различных проектах, играх, голосованиях, где могут проявить себя коалиции, поэтому можно определить сумму двух коалиционных структур и , полагая . Пусть всего в группе членов.

Вектор силы акционеров должен для каждой кооперативной игры указывать силу члена группы , при этом, он, очевидно, должен удовлетворять следующим естественным аксиомам:

1) если - коалиция-носитель, то ;

2) .

Разумеется, должны быть выполнены некоторые очевидные вещи, например, ничего не должно зависеть от того, как занумеровать членов группы.

Справедлива следующая теорема.

Теорема Шепли. Существует единственная вектор-функция , определенная для всех кооперативных игр и удовлетворяющая условиям 1-2).

Эта вектор-функция называется вектором Шепли - для каждой конкретной кооперативной игры это действительно упорядоченный набор чисел.

Доказательство этой теоремы достаточно сложное и опускается.

Приведем в явном виде выражение вектора Шепли . Сила -го акционера - соответствующая компонента вектора есть

)),

где есть число элементов . Обычно обозначают , тогда компоненты вектора Шепли можно записать в виде

(1)

Нетрудно видеть, что . Действительно,

. Величина есть число всех перестановок элементов группы, в которых элементу предшествуют только элемент коалиции , а все элементы не из этой коалиции стоят после . Множество всех таких перестановок, т.е. для всех коалиций, содержащих , есть, как легко видеть, множество вообще всех перестановок элементов группы, а их как раз ! .

Далее , по супераддитивности , следовательно, для всякого , тем самым вектор Шепли есть некоторый дележ рассматриваемой игры.

Вектору Шепли можно дать следующий содержательный смысл.

Предположим, что игроки ( акционеры) решили встретиться в определенном месте в определенное время. Однако из-за всякого рода случайностей они будут прибывать в некоторые случайные моменты времени, однако предполагается, что все порядки прибытия игроков (т.е. их перестановки) имеют одну и ту же вероятность, а именно, . Предположим, что игрок ,прибывая, застает только игроков коалиции и только их, тогда он получает , иначе говоря, его выигрышем является предельная величина, которую он вносит в коалицию.

Тогда компонента вектора Шепли представляет собой математическое ожидание выигрыша игрока в этой рандоминизационной схеме.

Можно придумать и другую подобную рандомизационную схему для пояснения содержательного смысла вектора Шепли. Все коалиции, содержащие элемент , разобъем в групп - по числу элементов в них. Игрок случайным образом выбирает коалицию, в которую он входит. Если он выбирает коалицию , то получает . Вероятность выбора коалиции с членами считаем равной произведению вероятности выбора группы - эту вероятность полагаем равной , на вероятность выбора конкретной коалиции из этой группы - эту вероятность полагаем равной ,

произведение этих вероятностей есть ,

т.е. выборы группы и коалиции из этой группы считаем независимыми. Тогда компонента вектора Шепли представляет собой математическое ожидание выигрыша игрока в этой рандоминизационной схеме. Эта схема, пожалуй, лучше объясняет содержательный смысл вектора Шепли, чем первая. Для простой кооперативной игры если выигрывающая коалиция, а нет, в остальных случаях . Поэтому для таких игр вектор Шепли вычисляется проще:

(2), где суммирование по распространяется на все такие выигрывающие коалиции , что не является выигрывающей.

Пример 1. Найдем вектор Шепли для коалиционной структуры из примера 2 из п.2.2. Напомним, что в этом примере речь идет об обладании контрольным пакетом среди четырех акционеров с 10,20,30 и 40 акциями. Уже знаем, что выигрышные коалиции есть {2,4},{3,4},{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}. При нахождении надо учесть, что единственная выигрышная коалиция , такая что не является выигрышной, есть коалиция {1,2,3}. Следовательно, так как =3, имеем =2!1!/3!=1/12 . Аналогично, находим, что коалиции {2,4}, {1,2,3} и {2,3,4} являются выигрышными, но перестают быть таковыми при удалении из них члена 2. Поэтому =1/12+1/12+1/12=1/4 . Точно также находим, что =1/4, =5/12 . Итак, вектор Шепли есть (1/12,1/4,1/4,5/12).

Этот вектор не совпадает с вектором "голосования", компоненты которого пропорциональны числу акций и который есть, стало быть, (1/10,1/5,3/10,2/5) . Заметим, что компоненты вектора Шепли для игроков 2 и 3 равны, хотя акций у игрока 3 больше. Это объясняется тем, что у игрока 3 не больше возможностей для образования выигрышных коалиций, чем у игрока 2. Кроме того, "сила" игрока 4 больше, чем доля его акций, а "сила" игрока 1 меньше его доли акций.

Если член группы есть "болван", то по определению,для любой коалиции , следовательно, компонента вектора Шепли для "болвана" равна 0. Легко видеть, что это есть характеристика "болвана".

2. Вектор Шепли в простом голосовании и в квалифицированном. И при простом и при квалифицированном голосовании имеем дело с простой симметричной игрой - см. конец п. 2.2, т.е. все члены группы совершенно равноправны, поэтому из соображений симметрии все компоненты вектора Шепли одинаковы, а так как их сумма равна 1, то все компоненты вектора Шепли равны , где - число членов группы. Подтвердим это прямыми вычислениями.

Вычислим вектор Шепли в простом голосовании. Для простоты пусть группа содержит 5 членов. Выигрывающие коалиции те, что содержат более 2 членов, однако те, что после удаления члена i перестают быть выигрышными, характеризуются очень просто - они содержат ровно 2 члена из подмножества , поэтому для любого члена группы имеем

Вычислим, далее, вектор Шепли для группы из 13 членов в случае голосования квалифицированным большинством - не менее 2/3 всех голосующих.

Выигрывающие коалиции те, что содержат 9 или более членов, однако коалиции, такие что после удаления члена перестают быть выигрышными, характеризуются очень просто - они содержат ровно 8 членов из подмножества , поэтому для любого члена группы имеем

Допустим, что в парламенте есть фракция, в которую входит более половины всех членов парламента. Во фракции железная дисциплина и при голосовании вся фракция голосует единогласно. Тогда любой член парламента, не входящий в эту фракцию, является "болваном", однако он вполне перестает быть таковым в процедурах голосования квалифицированным большинством.

3. Теорема Шепли. Естественно считать, что коалиция представляет своих членов в равной степени. Однако столь же естественно считать, что если кто-то является членом нескольких коалиций, то он не может быть активным членов всех этих коалиций и должен рассчитывать свои силы, разделяя их между разными коалициями. Припишем коалиции число между 0 и 1 и будем считать, что каждый член этой коалиции отдает ей -ю часть самого себя, так что это число разумно назвать степенью участия членов группы в этой коалиции. Обозначим тот набор коалиций, членом которых состоит.

Теперь можно дать следующее определение.

Набор коалиций называется сбалансированным, если каждой коалиции C набора можно приписать неотрицательное число ,(степень участия), так что

=1 для каждого (3)

Пример 2. Перечислим все сбалансированные наборы коалиций группы из трех участников (коалиции в фигурных скобках, наборы коалиций - в квадратных):

[{1,2,3}],[{1},{2},{3}],[{1},{2,3}],[{2},{3,1}],[{3},{1,2}],[{1,2}, {2,3}, {3,1}].

Первые пять наборов дизъюнктные. Заметим, что вообще дизъюнктные наборы, в которых коалиции охватывают всех членов являются сбалансированными наборами (для всех коалиций степень участия равна 1). Последний набор дизъюнктным не является, для коалиций из него степень участия равна 1/2 . Действительно, для нахождения степеней участия , имеем систему трех уравнений

Эта система имеет единственное решение: .

Однако в общем случае степени участия не определяются однозначно. Рассмотрим, например, набор . Мы можем приписать коалиции степень участия , где - произвольное число между 0 и 1 и положить - для любого .

Роль сбалансированных наборов в теории коалиций определяется замечательной теоремой Шепли, к формулировке которой переходим. Пусть - положительная константа, рассмотрим множество, это множество называется симплексом. Здесь - множество неотрицательных -мерных векторов. Любой коалиции сопоставим симплекс ,

для всех ,}, являющийся гранью симплекса .

Теорема Шепли. Пусть каждой коалиции сопоставлено такое замкнутое (возможно пустое) множество , чтодля всякого

(3)

Тогда существует такой сбалансированный набор коалиций , что.

Прокомментируем эту теорему. Предположим, что группа планирует разделить денежную сумму между своими членами. Тогда точки симплекса есть дележи этой суммы между членами группы.

Более того, симплекс , соответствующий коалиции есть множество дележей денежной суммы только между членами этой коалиции. Множество же есть множество дележей, приемлемых (или желательных) для коалиции (по определению! - если предложить какой-то дележ , то коалиция примет его, если и отвергнет в противном случае). При такой интерпретации, условие (3) утверждает, что есть множество приемлемых дележей для коалиции - поскольку , то каждый дележ из является приемлемым для какого-то члена коалиции или какой-то ее подкоалиции. В частности, весь симплекс тоже заполнен дележами, приемлемыми для какого-то члена группы или какой-то коалиции. Теорема Шепли утверждает, что при выполнении указанного условия (3) найдется сбалансированный набор коалиций , такой что . Пусть - какой-то вектор из этого пересечения, тогда для любой коалиции из этого набора. Таким образом, этот дележ приемлем для любой коалиции из набора и может быть рекомендован для "мирного разрешения" проблемы дележа, ради чего и формировались коалиции.

Набор коалиций для которого назовем совместным. Таким образом, теорема Шепли утверждает существование сбалансированного совместного набора коалиций при выполнении условия (3).

Пример 3. Заметим, что теорема не может утверждать существования дизъюнктного набора коалиций. Действительно, пусть 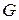G={1,2,3}, =1. Теперь определим замкнутые множества для всех возможных коалиций:

Можно проверить выполнение условия (3).

Но не существует дизъюнктного набора коалиций , такого что . В самом деле, существует только пять дизъюнктных наборов коалиций: , [{1},{2},{3}], [{1},{2,3}],[{2},{3,1}], [{3},{1,2}] однако каждый раз пересечение соответствующих множеств пусто.

Напротив, сбалансированный набор существует, как и утверждает теорема. Вот он:[{1,2},{2,3},{3,1}] - пересечение соответствующих множеств F свелось к точке (1/3,1/3,1/3).

Отметим также содержательный смысл множеств F в данном примере, например, означает, что коалиция{1,2} считает приемлемым для себя получить не менее 2/3 из всей единичной суммы.

Вопросы и задачи.

Задачи

1. Докажите, что коалиция, содержащая коалицию-носитель, сама является коалицией-носителем. Докажите, что если в конечной группе имеется коалиция-носитель, то она содержит минимальную коалицию-носитель (т.е эта последняя уже не содержит никакой отличной от себя коалиции-носителя).

2. Докажите, что в Примере 1 из §5.2 нет коалиции-носителя.

3. Может ли быть несколько коалиций-носителей? Может ли быть две дизъюнктных коалиций-носителей?

4. Пусть некоторая одночленная коалиция является носителем. Можно ли назвать единственного члена этой коалиции диктатором? Найдите характеристическую функцию такой коалиционной структуры.

5. Найдите вектор Шепли в борьбе за обладание контрольным пакетом четырех акционеров, обладающих 10,30,30 и 40 акциями. Есть ли здесь "болван"? Какова здесь коалиция-носитель?

6. В парламенте 450 депутатов, разбитых на пять фракций, в которых 180, 160, 40, 40, 30 депутатов. Найдите силу каждой фракции в голосовании простым большинством по выбору спикера (каждая фракция голосует солидарно: все "за" или все "против").

7. В группе из четырех человек трое равноправны, а четвертый - председатель, имеет два голоса. Оцените силу каждого члена группы в голосовании простым большинством и квалифицированном (не менее 2/3 всех голосов).

Ответ для голосования простым большинством: 1/6,1/6,1/6,1/2.

8. Пусть в группе из пяти человек два человека, например, 1-й и 2-й всегда голосуют единогласно. Найдите "силу" каждого члена группы (т.е. вектор Шепли) в процедуре простого голосования.

9. Найдите по соображениям симметрии вектор Шепли для игры из задачи 2 §5.2 и убедитесь, что этот вектор не принадлежит НМ-множеству, а ядро этой игры вообще пусто - см. ту же задачу.

10. Докажите, что для минимального сбалансированного набора коалиций степени участия коалиций определяются однозначно. При этом сбалансированный набор называется минимальным сбалансированным набором, если нет меньшего сбалансированного набора (т.е. при удалении хотя бы одной коалиции из такого набора он перестает быть сбалансированным).

11. Докажите, что каждый сбалансированный набор содержит минимальный сбалансированный набор.

12. Найдите все сбалансированные и все минимальные сбалансированные наборы коалиций в группе из четырех членов.

13. Убедитесь что в примере 3 замкнутые множества F для двучленных коалиций можно задать и так:

14. Пусть 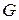={1,2,3}, =1 . Определим замкнутые множества Fдля всех возможных коалиций: Проверьте выполнение условия (3) из теоремы Шепли и найдите сбалансированный совместный набор коалиций. Каков содержательный смысл множеств F ?

КОНТРОЛЬНАЯ РАБОТА 3 (к Главам 4-5)

Текст задания, общего для всех вариантов, решение одного варианта и еще данные 10 подобных вариантов для самостоятельного решения.

Внимание! Вычисления вести либо в обыкновенных дробях, либо с точностью до 1-го знака после запятой.

1. Текст задания и данные к варианту № 1

1. Вычислить вектор Шепли при голосовании простым большинством при формировании контрольного пакета акций при распределении акций:.

2. Вычислить вектор Шепли в голосовании квалифицированным (более 2/3) большинством при формировании контрольного пакета акций при распределении акций:.

3.Вычислить прибыли фирм при выпусках при параметрах модели Курно ,.

Решения и указания.

1.См. пример 1 из §5.3.

2. См. п.2 из §5.3.

3. Имеем формулы для прибыли фирм при их выпусках: : 1-й 2-й: Подставляя, получаем:

Данные для дополнительных вариантов


20,20,20,20	20,20,20,20	10,20
20,30,30,20	20,30,30,20	15,15
10,10,10,70	10,10,10,70	20,10
5,15,25,55	5,15,25,55	16,4
5,15,25,55	5,15,25,55	27,3
70,10,5,15	70,10,5,15	10,10
70,10,5,15	70,10,5,15	10,20
10,10,0,80	10,10,0,80	15,25
10,10,0,80	10,10,0,80	15,35
90,5,5,0	90,5,5,0	20,20

§5.4.Теоремы Шепли и Скарфа и их роль в научной организации труда()

1.Пример 1; 2.Комментарий к вектору Шепли;3. Пример 3; 4.Теорема Скарфа; 5.Роль теорем Шепли и Скарфа в научной организации труда;

Вопросы и задачи

Пример 1. Рассмотрим небольшую автомастерскую, занимающуюся мелким ремонтом автомобилей. В мастерской всего 5 человек : две бригады по 2 человека, работающих вместе и один человек, занимающийся закупкой запчастей и всякими необходимым расчетами (ведением бухгалтерского учета в том числе). Этому особому члену мастерской присвоим код 0 и назовем его условно начальником мастерской, а бригадам – коды 1,2 (бригады совершенно одинаковы).

Каждая бригада работает только в полном составе – в составе 2-х человек. Любая коалиция должна включать только полную бригаду или не включать ни одного члена из этой бригады, так что коалиции таковы: пустая коалиция , одночленные {0}, {1}, {2}, двучленные {0,1},{0,2},{1,2} и одна трехчленная {0,1,2}. Выигрыш коалиции – это получаемая коалицией прибыль. Эти прибыли – значения функции таковы: Объяснения этих чисел таковы: сам по себе начальник делать ничего особо не умеет, поэтому, работая в одиночестве, он может за месяц заработать только 6000 руб. Каждая из бригад, работая обособленно, может заработать на бригаду 40000 руб, так как их работа не очень эффективна – они вынуждены все время отвлекаться на покупку запчастей и т.п.. Если бригада работает вместе с начальником , то они вместе заработают 60000 руб. Если же мастерская работает в полном составе, то работа мастерской весьма эффективна – они вместе зарабатывают 120 000 руб.

Для распределения заработка между работниками мастерской подсчитаем компоненты вектора Шепли. Напомним, что они задаются формулой:

(1).

Поясним смысл входящих в эту формулу величин. Здесь - число членов рассматриваемой группы, - число членов коалиции , в которую входит рассматриваемый член группы, обозначает выигрыш, который может обеспечить себе (произвольная) коалиция , следовательно, - это дополнительный выигрыш, который может обеспечить член при вхождении его в коалицию (тем самым она превращается в коалицию ), и, наконец, и есть то самое количественное выражение силы члена группы.

Их три , но в силу одинаковости бригад , так что нужно найти только .

Коалиций, содержащих 0 всего 4: {0},{0,1},{0,2},{0,1,2}. Тогда

=руб.

Коалиций, содержащих 1 всего 4:{1},{0,1},{1,2},{0,1,2}. Тогда

49000 руб.

Эти числа 22000 и 49000 есть количественное выражение «силы» или ценности соответственно начальника и каждой из бригад и величина их заработка. Таким образом, начальник получит 22000 руб., а каждый член каждой бригады получит по 24500 руб. То что сумма заработков равна 120000 руб. не случайно – это следствие свойств вектора Шепли.

2.Комментарий к вектору Шепли.Вектор Шепли можно использовать не только для распределения заработка между работниками, как в только что рассмотренном примере. Его можно использовать, например, для распределения годового вознаграждения между топ-менеджерами компании с учетом их должностей, влиятельности, возможностей «лоббирования» и т.д. Да так в реальности и происходит, только, конечно, без скрупулезного вычисления компонент вектора Шепли. Вектор Шепли можно использовать для распределения машин и механизмов между бригадами и подразделениями. Ведь основная идея вектора Шепли- как усиливает бригаду включение в нее того или иного работника, действует и в этом случае –в случае машин и механизмов. Даже распределение полномочий между подразделениями фирмы может использовать эту идею о дополнительном усилении! Кстати, идея о дополнительном усилении давно используется в других областях. Например, при распределении ресурсов между предприятиями можно использовать двойственные оценки ресурсов: ведь двойственная оценка ресурса на данном предприятии показывает сколько дополнительной прибыли приносит вовлечение в производство на этом предприятии еще одной единицы этого ресурса (см.§2.4).

Пример 3. Иванов (И), Петров (П) и Сидоров (С) занимаются частным извозом. В их распоряжении автомобиль ВАЗ – такси и грузовик «Газель». Иванов имеет много знакомств и хорошо знает город, поэтому когда он работает таксистом, то зарабатывает за смену 1200 руб, Петров – 1000 руб и Сидоров – 800 руб. Когда Иванов и Петров работают на грузовике, то зарабатывают за смену 3600 руб, Иванов и Сидоров – 3200 руб и Петров и Сидоров - 3000 руб. Как им нужно работать и как распределить заработанное?

Решение. Возможны три варианта: Иванов – таксист, Петров и Сидоров - на грузовике; Петров – таксист, Иванов и Сидоров – на грузовике и, наконец, Сидоров – таксист, Иванов и Петров – на грузовике. Несложные подсчеты показывают, что самый выгодный – 3-й вариант и в этом варианте их заработок за смену составляет 4400 руб. Для распределения этой суммы между Ивановым, Петровым и Сидоровым применим вектор Шепли.

Для Сидорова возможные коалиции есть {С, СИ,СП,СИП} и

1200 руб. Для Петрова возможные коалиции есть

{П, ПИ,ПС,ПИС} и

руб. Для Иванова возможные коалиции есть

{И,ИП,ИС,ИПС} и

руб.

Разница в зарплате между Ивановым и Сидоровым получилась почти полуторная! Но, ведь с другой стороны, таксистом Иванов и зарабатывал бы в 1,5 раза больше Сидорова-таксиста! Да и вряд ли Сидоров будет протестовать – ведь работая таксистом, он вносит в общий заработок всего 800 руб, а получает из этого общего заработка 1200 руб! И все же в этом примере что-то не то. А, понятно – ведь Иванов и Петров окажутся недовольны – 400 руб из своего заработка на грузовике они отдают Сидорову! Так долго продолжаться не может, коалиция {Иванов, Петров} взорвет ситуацию. Говоря научным языком – коалиция эта блокирует дележ {1700, 1500,1200}.

Докажем, что ядро данной игры пусто. Предположим, что (И, П, С) – какой-нибудь дележ, тогда

И+П+С=4400

Если этот дележ недоминируемый (что и означает непустоту ядра), то двучленные коалиции дают три неравенства:

И+П3600, П+С3000, С+И3200.

Складывая эти неравенства, получим (И+П+С), что противоречит равенству И+П+С=4400

Имеем пример того, что вектор Шепли не принадлежит к ядру игры (потому, что оно вообще пусто!) и потому не может служить универсальным способом подсчета «силы» игрока.

Итак, ядро игры пусто, поэтому Иванову, Петрову и Сидорову придется нелегко – они не сумеют договориться о том, как им работать и делить совместный заработок. Не помогут даже некоторые ухищрения, рекомендуемые теорией игр. Например, можно рассмотреть обобщение ядра игры, так называемые -решения игры. Напомним, множество дележей обозначается .

Множество называется -решением, если

1)ни один из дележей, входящих в не доминирует никакой дележ из ;

2)всякий дележ, не входящий в доминируется некоторым дележом из .

Пусть. Докажем, что есть НМ-решение. Во-первых, в нет двух дележей, один из которых доминирует другой, т.е. условие 1) выполнено. Пусть - какой-нибудь дележ, тогда . Если , то . Рассмотрим дележ , очевидно, что этот дележ из и он доминирует дележ по коалиции {И,П}. Если же , но тогда дележ . Легко видеть, что каждое из следующих двух множеств дележей есть -решение. Доказательство аналогично. Мы видим, что -решения разительно отличаются от недоминируемых дележей. Неясен даже содержательный смысл -множества. Можно только сказать, что в -множестве собраны лучшие дележи (так можно не совсем точно перефразировать условие 2)) и нет «лишних» дележей ( так можно перефразировать условие 1)). Можно также сказать, что при любом разумном подходе к понятию дележа приемлемый для всех коалиций дележ должен лежать в любом - множестве (напомним, что ядро всегда лежит в любом -множестве). Кстати, из этого следует, что пересечение всех -множеств содержит ядро. Так как пересечение указанных выше трех -множеств пусто, то это еще раз доказывает, что ядро этой игры (из примера 3) пусто. Не удалось установить, совпадает ли ядро игры с пересечением всех -множеств в общем случае.

Не поможет нашей троице и возможность побочных платежей. Суть в том, что побочные платежи не уменьшают сумму заработков двучленных плюс одночленных коалиций, поэтому справедливы неравенства (которые справедливы еще и из-за свойства супераддитивности!):

И+П+С3600+800, П+С+И3000+1200, С+И+П3200+1000,

и они по-прежнему противоречат равенству И+П+С=4400

Рассматриваемый пример наводит на простую мысль – чтобы рабочий коллектив состоялся, необходим синергетический эффект – чтобы вместе коллектив зарабатывал больше чем любые дизъюнктные коалиции в сумме. Т.е. Иванову, Петрову и Сидорову вместе должно работать выгоднее, чем поодиночке. Например, пусть Сидоров любит работать вечером таксистом, а днем он по телефону принимает заказы для Иванова и Петрова, так что суммарный заработок их увеличится с 4400 руб. до 5000 руб. Повторив вышеприведенные расчеты для этого случая, получим распределение заработка 5000 руб - {1900, 1700, 1400}. Это уже лучше! В самом деле, легко убедиться, что полученный дележ является недоминируемым, что и означает непустоту ядра.

Вернемся к теореме Скарфа. Набор коалиций называется сбалансированным, если каждой коалиции набора можно приписать неотрицательное число , (степень участия в ней членов коалиции), так что для каждого .

Заметим, что если все равны 0 или 1, то такой набор коалиций есть просто разбиение группы 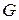на дизъюнктные коалиции.

(Понятие сбалансированного набора коалиций введено в [14].)

На понятие сбалансированного набора можно взглянуть с обычной житейской точки зрения: редко какой человек работает на одной работе и с полной отдачей. Обычно человек работает на нескольких работах (или имеет несколько занятий, например, кроме основной работы пишет романы, поет в церковном хоре или подрабатывает частным извозом) и вынужден распределять свои силы и время между этими работами. Число и показывает, какую часть «самого себя» человек отдает работе .

На кооперативную игру можно посмотреть как на некоторую «экономику» (об этом взгляде см. [3]). Тогда коалиции можно рассматривать как фирмы, конкурирующие за работников – игроков. Фирмы заманивают игроков «зарплатой», на которую коалиция имеет фонд . Игроки «продают» фирмам единственный ресурс, который они имеют – свой труд. Условно, запас этого ресурса у каждого игрока примем за . Пусть - сбалансированный набор коалиций, и коалиция принадлежит этому набору, тогда каждый игрок, входящий в эту коалицию «продает» коалиции долю своего ресурса – своего фонда труда (это – некоторое нарушение реальности: вовсе не с одной и той же интенсивностью работаем мы на разных работах!). Таким образом, условие сбалансированности набора , которое выполняется для каждого работника означает, что он «продает» коалициям набора в точности весь свой труд, т.е. он полностью занят на всех работах, входящих в набор.

Рассмотрим какой-нибудь дележ . Если для коалиции выполняется условие , то коалиция не может обеспечить требуемые работниками «зарплаты» - эти требуемые зарплаты превышают в сумме ее «фонд зарплаты», такая коалиция не может функционировать в составе данного сбалансированного набора, и тогда надо считать, что .

Напомним кое-что необходимое из теории кооперативных игр . Пусть - два дележа. Говорят, что дележ доминирует дележ по коалиции (обозначается ) если

1) и

2) для всех .