Коэффициент эластичности показывает

a)На сколько % изменится результат при изменении фактора на 1%

b)На сколько ед. изменится фактор при изменении результата на 1 ед.

c)На сколько ед. изменится результат при изменении фактора на 1 ед.

d)Во сколько раз изменится результат при изменении фактора на 1 ед.

e)На сколько % изменится фактор при изменении результата на 1%

21. Для построения модели линейной множественной регрессии вида необходимое количество наблюдений должно быть не менее:

a)2;

b)7;

c)14.

22. Аддитивная модель временного ряда имеет вид:

a) ;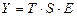

b) ;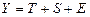

c) .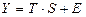

23. Мультипликативная модель временного ряда имеет вид:

a) ;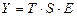

b) ;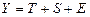

c) .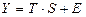

24. Тенденция временного ряда характеризует совокупность факторов, …

a) оказывающих долговременное влияние и формирующих общую динамику изучаемого показателя

b) оказывающих сезонное воздействие

c) оказывающих единовременное влияние

d) не оказывающих влияние на уровень ряда

25. Представление уровней временного ряда в виде , где 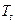- тренд, 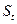– сезонная компонента, – случайная компонента соответствует:

a)мультипликативной модели

b)аддитивной модели

c)модели смешанного типа

ВАРИАНТ 2.

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

а) аналитический;

б) графический;

в) экспериментальный (табличный).

2. Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

а) не менее 5 наблюдений;

б) не менее 7 наблюдений;

в) не менее 10 наблюдений.

3. Суть метода наименьших квадратов состоит в:

а) минимизации суммы остаточных величин;

б) минимизации дисперсии результативного признака;

в) минимизации суммы квадратов остаточных величин.

4. Коэффициент линейного парного уравнения регрессии:

а) показывает среднее изменение результата с изменением фактора на одну единицу;

б) оценивает статистическую значимость уравнения регрессии;

в) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

5. На основании наблюдений за 50 семьями построено уравнение регрессии 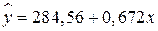, где 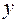– потребление, 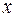– доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

а) да;

б) нет;

в) ничего определенного сказать нельзя.

6. Суть коэффициента детерминации 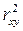состоит в следующем:

а) оценивает качество модели из относительных отклонений по каждому наблюдению;

б) характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака;

в) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

7. Качество модели из относительных отклонений по каждому наблюдению оценивает:

а) коэффициент детерминации ;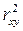

б) -критерий Фишера;

в) средняя ошибка аппроксимации .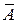

8. Значимость уравнения регрессии в целом оценивает:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .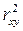

9. Классический метод к оцениванию параметров регрессии основан на:

а) методе наименьших квадратов:

б) методе максимального правдоподобия:

в) шаговом регрессионном анализе.

10. Остаточная сумма квадратов равна нулю:

а) когда правильно подобрана регрессионная модель;

б) когда между признаками существует точная функциональная связь;

в) никогда.

11. Для оценки значимости коэффициентов регрессии рассчитывают:

а) -критерий Фишера;

б) -критерий Стьюдента;

в) коэффициент детерминации .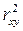

12. Какое уравнение регрессии нельзя свести к линейному виду:

а) ;

б) :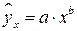

в) .

13. Какое из уравнений является степенным:

а) ;

б) :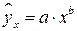

в) .

14. Параметр в степенной модели является:

а) коэффициентом детерминации;

б) коэффициентом эластичности;

в) коэффициентом корреляции.

15. Коэффициент корреляции может принимать значения:

а) от –1 до 1;

б) от 0 до 1;

в) любые.

16. Какое из следующих уравнений нелинейно по оцениваемым параметрам:

а) ;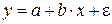

б) ;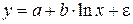

в) .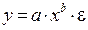

17. Добавление в уравнение множественной регрессии новой объясняющей переменной:

а) уменьшает значение коэффициента детерминации;

б) увеличивает значение коэффициента детерминации;

в) не оказывает никакого влияние на коэффициент детерминации.

18. Множественный коэффициент корреляции 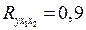. Определите, какой процент дисперсии зависимой переменной объясняется влиянием факторов и :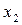

а) 90%;

б) 81%;

в) 19%.

19. Для построения модели линейной множественной регрессии вида 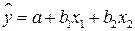необходимое количество наблюдений должно быть не менее:

а) 2;

б) 7;

в) 14.

20. Стандартизованные коэффициенты регрессии :

а) позволяют ранжировать факторы по силе их влияния на результат;

б) оценивают статистическую значимость факторов;

в) являются коэффициентами эластичности.

21. Укажите истинное утверждение:

а) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;

б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;

в) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.

22. Коэффициент автокорреляции:

а) характеризует тесноту линейной связи текущего и предыдущего уровней ряда;

б) характеризует тесноту нелинейной связи текущего и предыдущего уровней ряда;

в) характеризует наличие или отсутствие тенденции.

23. Аддитивная модель временного ряда строится, если:

а) значения сезонной компоненты предполагаются постоянными для различных циклов;

б) амплитуда сезонных колебаний возрастает или уменьшается;

в) отсутствует тенденция.

24. Мультипликативная модель временного ряда строится, если:

а) значения сезонной компоненты предполагаются постоянными для различных циклов;

б) амплитуда сезонных колебаний возрастает или уменьшается;

в) отсутствует тенденция.

25. На основе поквартальных данных построена аддитивная модель временного ряда. Скорректированные значения сезонной компоненты за первые три квартала равны: 7 – I квартал, 9 – II квартал и –11 – III квартал. Значение сезонной компоненты за IV квартал есть:

а) 5;

б) –4;

в) –5.