Применение метода гармонической линеаризации для определения режима автоколебаний.

Рис. 4.48.

Если система находится в режиме автоколебаний, то на входе в нелинейный элемент сигнал 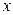является синусоидой:

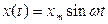(4.34)

На выходе нелинейного элемента сигнал 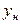имеет вид периодического сигнала, в общем случае отличного от синусоидального. Уравнение такого сигнала имеет вид:

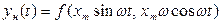(4.35)

Известно, что любой периодический сигнал может быть разложен в ряд Фурье и тем самым представлен в виде суммы гармонических составляющих:

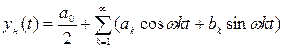(4.36)

где 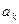,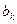- коэффициенты ряда Фурье определяются по формулам :

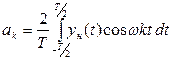(4.37)

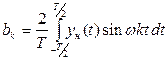(4.38)

где Т – период повторения сигнала.

Однако уравнения (4.36) можно упростить, если учитывать следующее:

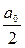1. Статические характеристики большинства нелинейных элементов являются кососимметричными, т.е. симметричными относительно начала координат (). В этом случае постоянная составляющая и коэффициенты всех четных гармоник равны нулю().

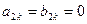2. Линейная часть нелинейных систем, которая располагается за нелинейным элементом, выполняет роль фильтра низких частот, т.е. на выходе нелинейной системы гасятся все гармоники кроме первой.

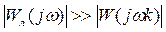(4.39)

 

3,5....

На основе этих предпосылок уравнение (4.36) приобретает вид:

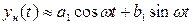(4.40)

 

Из уравнения (4.34) можно получить:

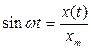(4.41)

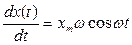(4.42)

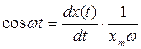(4.43)

Тогда уравнение (4.40) имеет вид:

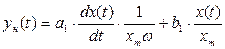(4.44)

Введем обозначения:

 

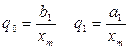(4.45)

 

С учетом (4.45) уравнение (4.44) имеет вид:

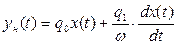(4.46)

или в операторном виде:

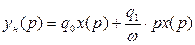(4.47)

 

Таким образом, при выполнении указанных выше допущений нелинейное уравнение (4.35) может быть заменено линейным уравнением (4.46)или (4.47). Эта операция называется гармонической линеаризацией , уравнение (4.46) –уравнением гармонической линеаризации, а коэффициенты 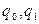- коэффициентами гармонической линеаризации. Коэффициенты гармонической линеаризации зависят от вида нелинейной характеристики 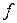и могут быть определены по формулам (4.37), (4.38), (4.45).

Коэффициенты наиболее часто встречающихся нелинейных элементов приведены в таблице.*

Значения коэффициентов гармонической линеаризации.

 

Нелинейный элемент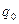

 

 

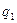
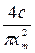
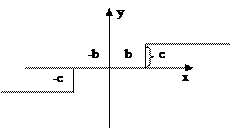
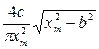
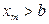
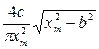
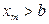
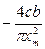
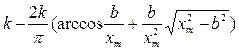
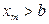
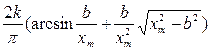
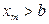
Гармоническая линеаризация принципиально отличается от обычной линеаризации. При гармонической линеаризации:

· коэффициенты гармонической линеаризаци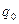и и 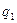не являются постоянными, а зависят от амплитуды входного сигнала .

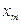· Уравнение гармонической линеаризации содержит две составляющие: входной сигнал и его производную.

 

Применяя гармоническую линеаризацию на вышеприведенных допущениях можно исследовать устойчивость системы методами теории устойчивости линейных систем.

Рассмотрим типовую нелинейную систему. Передаточная функция линейной части имеет вид:

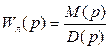(4.48)

Эквивалентную передаточную функцию нелинейного элемента можно получит из (47):

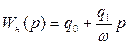(4.49)

Тогда передаточная функция замкнутой системы имеет вид:

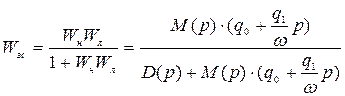(4.50)

А характеристическое уравнение гармонически линеаризованной системы имеет вид:

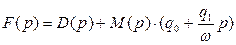(4.51)

Наиболее удобно исследовать автоколебания при помощи критерия Михайлова:

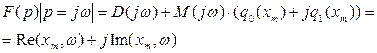(4.52)

Согласно критерию устойчивости Михайлова в системе установятся колебания с постоянной амплитудой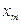и частотой 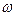, если годограф Михайлова проходит через начало координат, т. е. когда и мнимая и действительная части характеристического полинома одновременно равны нулю:

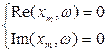(4.53)

Разрешая данную систему уравнений относительно 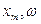, можно определить возможность возникновения автоколебаний в системе. Если уравнения (4.53) не имеют положительных корней , то автоколебания в системе невозможны.

Если 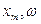положительные величины, то системе возможен режим колебания с постоянной амплитудой. Определить, являются ли данные колебания автоколебаниями, можно с помощью дополнительных исследований.

Изучая фазовые траектории, соответствующие режиму автоколебаний, можно сделать следующий вывод: что в режиме автоколебаний при увеличении амплитуды 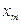на величину 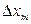в системе происходил сходящийся процесс к величине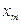; а при уменьшении на 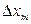происходил расходящийся процесс до величины 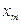. Аналогичные процессы происходят при изменении частоты .

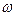Для дополнительных исследований на устойчивость колебаний применяются критерии устойчивости: Гурвица, Михайлова и Найквиста.