Метод гармонической линеаризации.

Рис. 4.47.

Рис. 4.46.

Рис. 4.45.

Рис. 4.44.

Рис. 4.43.

Рис. 4.42.

Рис. 4.41.

Рис. 4.40.

Рис. 4.39.

Рис. 4.38.

Рис. 4.37.

Рис. 4.36.

Рис. 4.35.

Рис. 4.34.

Рис. 4.33.

Рис. 4.32.

Фазовая траектория для данного переходного процесса имеет вид:

 

 

Устойчивый апериодический переходный процесс имеет вид:

 

 

 

Фазовая траектория для данного переходного процесса имеет вид:

 

Неустойчивый колебательный переходный процесс имеет вид:

 

 

 

Фазовая траектория для данного переходного процесса имеет вид:

 

 

Неустойчивый апериодический переходный процесс имеет вид:

 

 

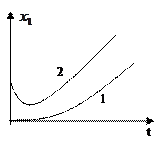Фазовая траектория для данного переходного процесса имеет вид:

 

Система, находящаяся на границе колебательной устойчивости, имеет переходный процесс:

 

 

 

 

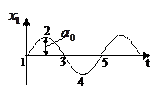Фазовая траектория для данного переходного процесса имеет вид:

 

 

 

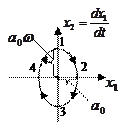Рассмотрев фазовые траектории для линейных систем можно сделать следующие выводы:

§ В верхних квадрантах фазовой плоскости изображающая точка движется всегда слева направо, а в нижних – справа налево. Это объясняется тем, что при переменная возрастает, а при 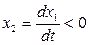переменная убывает.

§ В любой точке фазовой плоскости, где переменная и функция не равны нулю, фазовая траектория имеет только одно определенное направление, соответствующее значению производной 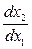в данной точке. Из этого следует, что фазовые траектории в таких точках не пересекаются.

§ Если 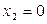, то , т. е. фазовые траектории пересекают ось под прямым углом, а переменная достигает своего максимума. Если при 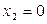одновременно 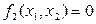, то фазовая траектория в таких точках не имеет определенного направления, а обе производные и равны нулю. (18). Последнее означает, что изображающая точка неподвижна, а исследуемая система управления находится в состоянии равновесия. Такие точки называются особыми.

§ Если переходный процесс является сходящимся, что соответствует устойчивым система, то фазовая траектория имеет вид либо скручивающейся к началу координат спирали (для колебательного процесса), либо дуги, сходящейся к началу координат (для апериодического процесса);

§ Если система неустойчива, то фазовая траектория - раскручивающаяся спираль или расходящаяся дуга;

§ Если в системе установились колебания с постоянной амплитудой и частотой, то фазовой траекторией является эллипс, который называется предельным циклом.. По параметрам эллипса можно определить амплитуду и частоту;

§ Для всех фазовых траекторий характерны следующие особенности: в верхних квадрантах плоскости фазовые траектории имеют направление слева направо; в нижнем квадранте – справа налево

 

Свойства фазовых траекторий для линейных систем сохраняются и для фазовых траекторий нелинейных систем. Однако фазовые траектории нелинейных систем имеют свои особенности.

 

4.5.1.3. Особенности нелинейных систем:

 

§ В нелинейных системах, как правило, рассматривают фазовый портрет системы, т. е. совокупность фазовых траекторий, соответствующих различным начальным условиям.

§ Нелинейные элементы изменяют фазовые траектории, например фазовые траектории нелинейных систем с нелинейностями типа «реле» имеют изломы в линии, называемой линией переключения

§ Если нелинейный элемент имеет зону нечувствительности, то фазовый портрет нелинейной системы имеет множество особых точек, которые определяют отрезок равновесия.

 

 

 

§ Режиму автоколебаний соответствует фазовый портрет, на которм фазовые траектории сходятся к предельному циклу.

 

 

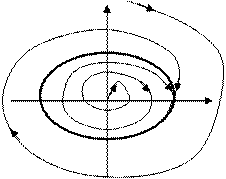§ Для систем устойчивых в малом, но неустойчивых в большом фазовый портрет имеет вид, при котором фазовые траектории, внутри предельного цикла сходятся к началу координат, а вне предельного цикла расходятся от предельного цикла. Предельный цикл в данном случае является неустойчивым.

 

 

Метод фазовых траекторий графическим методом дает наглядное изображение устойчивости систем и определения режима автоколебания.

В отличие от линейных систем в нелинейных может быть несколько режимов автоколебания, что соответствует нескольким предельным циклам. Параметры предельного цикла определяют параметры автоколебания (амплитуду и частоту). Однако метод фазовых траекторий удобен для исследования систем второго и третьего порядков, поэтому этот метод имеет ограниченное использование.

 

ПРИМЕР

Построить фазовый портрет для следующей системы

 

 

Где , а нелинейный элемент – реле, имеющий статическую характеристику :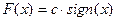

 

 

 

Уравнение (4.12) можно переписать в виде

 

(4.27)

Если входной сигнал – единичное ступенчатое воздействие, то (27) принимает вид

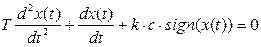(4.28)

 

Введем новые фазовые переменные:

(4.29)

Уравнение фазовых траекторий имеет вид:

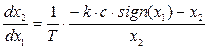(4.30)

При 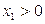уравнение имеет вид:

(4.31)

При уравнение имеет вид:

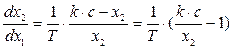(4.32)

Разрешив такие уравнения при заданных начальных условиях 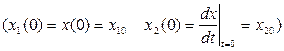можно получить уравнение для фазовых траекторий:

Для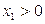

(4.33)

Для

(4.33)

 

Метод гармонической линеаризации является приближенным методом исследования режима автоколебаний нелинейных систем. Этим методом можно определить условия возникновения и параметры автоколебаний как в системах второго порядка, так и в более сложных системах.

Метод основан на замене существенно нелинейного элемента системы эквивалентным линейным звеном. В замкнутой автоматической системе, работающей в режиме автоколебаний. Условием эквивалентности служит равенство амплитуд и фаз выходного сигнала эквивалентного звена и первой гармоники выходного сигнала реального нелинейного элемента. При этом предполагается, что сигнал на входе нелинейного элемента является синусоидальным. Такое предположение справедливо во всех случаях, когда линейная часть системы достаточно инерционна и не пропускает высокочастотные гармоники.

Рассмотри м типовую нелинейную систему