Формы итогового контроля.

В соответствии с учебными планами по специальности «Финансы и кредит» и «Бухгалтерский учет, анализ и аудит», для всех категорий студентов формой итогового контроля по курсу «Эконометрика» является зачет, предполагающий:

1. Ответ на теоретический вопрос

2. Ответ на вопрос теста

3. Решение задачи по тематике курса.

Вопросы для подготовки к зачету

1. Понятие эконометрики модели. Примеры. Типы переменных.

2. Этапы эконометрического моделирования. Задачи. Проблемы. Методы.

3. Методы наименьших квадратов оценивания коэффициентов регрессии.

4. Какова концепция F-критерия Фишера?

5. t-критерий Стьюдента проверки статистической значимости оценок коэффициентов регрессии.

6. Построение доверительных интервалов для коэффициентов регрессии.

7. Как оценивается значимость параметров уравнения регрессии?

8. Запишите все виды моделей, нелинейных относительно:

– включаемых переменных,

– оцениваемых параметров.

9. В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров?

10. Процедура линеаризации. Примеры.

11. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?

12. В чем состоит спецификация модели множественной регрессии?

13. Сформулируйте требования, предъявляемые к факторам для включения их в модель множественной регрессии.

14. К каким трудностям приводит мультиколлинеарность факторов, включаемых в модель?

15. Назовите методы устранения мультиколлинеарности факторов.

16. Составьте матрицу частных коэффициентов корреляции разного порядка для регрессионной модели с четырьмя факторами.

17. Как связаны между собой t-критерии Стьюдента для оценки значимости b_i и частные F-критерии?

18. Сформулируйте основные предпосылки применения МНК для построения регрессионной модели.

19. Как можно проверить наличие гомо- или гетероскедастичности остатков?

20. Как оценивается отсутствие автокорреляции остатков при построении регрессионной модели.

21. Понятие автокорреляции. Критерий Дарбина-Уотсона.

22. Назовите возможные способы построения системы уравнений.

23. Как связаны между собой структурная и приведенная формы моделей?

24. В чем состоит проблема идентификации модели, какие условия идентификации вы знаете?

25. В чем суть косвенного метода наименьших квадратов?

26. В каких случаях применяется двухшаговый метод наименьших квадратов?

27. Перечислите основные элементы временного ряда.

28. Дайте определения автокорреляционной функции временного ряда.

29. Перечислите основные виды трендов.

30. Выпишите общий вид мультипликативной и аддитивной модели временного ряда.

Варианты тестов по дисциплине

ВАРИАНТ 1.

1. Наиболее наглядным видом выбора уравнения парной регрессии является:

a) аналитический;

b) графический;

c) табличный.

2. Линейная однофакторная модель содержит число коэффициентов, равное:

a)2

b)3;

c)4;

d)1;

3. Теоретическими значениями называются:

a)значения результативного признака, вычисленные по уравнению регрессии

b)фактические значения результативного признака

c)фактические значения факторного признака

4. Суть метода наименьших квадратов состоит в:

a)минимизации суммы остаточных величин;

b)минимизации дисперсии результативного признака;

c)минимизации суммы квадратов остаточных величин.

5. Коэффициент линейного парного уравнения регрессии:

a)показывает среднее изменение результата с изменением фактора на одну единицу;

b)оценивает статистическую значимость уравнения регрессии;

c)показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

6. Коэффициент b_i уравнения регрессии показывает

a)На сколько ед. изменится результат при изменении фактора на 1 ед.

b)На сколько % изменится результат при изменении фактора на 1%

c)На сколько % изменится фактор при изменении результата на 1%

d)На сколько ед. изменится фактор при изменении результата на 1 ед.

e)Во сколько раз изменится результат при изменении фактора на 1 ед.

7. Коэффициент корреляции 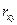может принимать значения:

a)от –1 до 1;

b)от 0 до 1;

c)любые.

8. Нулевая гипотеза для коэффициента регрессии b в уравнении парной линейной регрессии 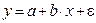проверяется с помощью

a)статистики Стьюдента;

b)стандартного нормального распределения;

c)статистики Фишера;

d)распределения Пуассона.

9. Если между величинами X и Y существует положительная, но не функциональная связь, то парный коэффициент корреляции находится в пределах:

a)от –1 до 0

b)от 0 до 1

c)не меньше 1

d)не больше –1.