Первая нормальная форма

Труднее всего дать определение вещей, которые всем понятны. Если давать не строгое, описательное определение, то всегда остается возможность неправильной его трактовки. Если дать строгое формальное определение, то оно, как правило, или тривиально, или слишком громоздко. Именно такая ситуация с определением отношения в Первой Нормальной Форме (1НФ). Совсем не говорить об этом нельзя, т.к. на основе 1НФ строятся более высокие нормальные формы, которые рассматриваются далее в гл. 6 и 7. Дать определение 1НФ сложно ввиду его тривиальности. Поэтому, дадим просто несколько объяснений.

Объяснение 1. Говорят, что отношение 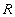находится в 1НФ, если оно удовлетворяет определению 2.

Это, собственно, тавтология, ведь из определения 2 следует, что других отношений не бывает. Действительно, определение 2 описывает, что является отношением, а что - нет, следовательно, отношений в непервой нормальной форме просто нет.

Объяснение 2. Говорят, что отношение 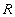находится в 1НФ, если его атрибуты содержат только скалярные (атомарные) значения.

Опять же, определение 2 опирается на понятие домена, а домены определены на простых типах данных.

Непервую нормальную форму можно получить, если допустить, что атрибуты отношения могут быть определены на сложных типах данных - массивах, структурах, или даже на других отношениях. Легко себе представить таблицу, у которой в некоторых ячейках содержатся массивы, в других ячейках - определенные пользователями сложные структуры, а в третьих ячейках - целые реляционные таблицы, которые в свою очередь могут содержать такие же сложные объекты. Именно такие возможности предоставляются некоторыми современными пост-реляционными и объектными СУБД.

Требование, что отношения должны содержать только данные простых типов, объясняет, почему отношения иногда называют плоскими таблицами (plain table). Действительно, таблицы, задающие отношения двумерны. Одно измерение задается списком столбцов, второе измерение задается списком строк. Пара координат (Номер строки, Номер столбца) однозначно идентифицирует ячейку таблицы и содержащееся в ней значение. Если же допустить, что в ячейке таблицы могут содержаться данные сложных типов (массивы, структуры, другие таблицы), то такая таблица будет уже не плоской. Например, если в ячейке таблицы содержится массив, то для обращения к элементу массива нужно знать три параметра (Номер строки, Номер столбца, Номер элемента в массиве).

Таким образом появляется третье объяснение Первой Нормальной Формы:

Объяснение 3. Отношение 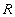находится в 1НФ, если оно является плоской таблицей.

Мы сознательно ограничиваемся рассмотрением только классической реляционной теории, в которой все отношения имеют только атомарные атрибуты и заведомо находятся в 1НФ.