Центральное растяжение - сжатие. Закон Гука.

Напряжение, перемещение, деформации.

ВСФ, определяется с помощью метода сечения.

Классификация сил и нагрузок. Метод сечений.

Допущения и гипотезы в сопротивлении материалов.

Реальный объект и расчетная схема изучаемого объекта.

Структура дисциплин механического цикла

Реальный объект, освобожденный от несущественных особенностей, называется расчетной схемой.

Виды тел:

· Брус

Брусом называется геометрическое тело, два размера которого намного меньше его третьего размера.

Брусья бывают:

· прямолинейные;

· криволинейные;

· с постоянным сечением;

с переменным сечением;

с комбинированным сечением.

Примеры: балки, оси, валы, стержни, крюки, брусья, звенья цепей и т. д.

· Оболочка

Оболочкой называется геометрическое тело, длина и ширина которого значительно больше её толщины.

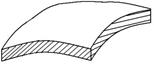Оболочки бывают:

· тонкостенными;

· толстостенными.

По форме различают:

· цилиндрические;

· конические;

· сферические.

Примеры:резервуары для хранения нефтепродуктов и газа, трубопроводы, купола зданий, корпуса машин, самолетов, судов

и т.д.

· Пластина

Пластиной называется оболочка с плоской поверхностью.

Примеры: плоские днища и крышки резервуаров, перекрытия инженерных сооружений, диски турбомашин.

· Массив

Массивом называется геометрическое тело, все три размера которого величины одного порядка.

Примеры: парапеты, фундамент зданий и т.д.

Допущения о свойствах материалов и допущения о деформации.

1. Допущение о сплошности (понятие, предполагающее, что материал полностью заполняет занимаемый им объем);

2. Допущение об однородности (одинаковость свойств материала во всех его точках);

3. Изотропность (одинаковость свойств материала во всех напряжениях: сталь – изотропна, дерево - анизотропно);

4. Допущение об идеальной упругости (полностью восстанавливать форму и размеры после устранения причин, вызывающих эти изменения: силовые воздействия, температурные воздействия).

Деформации бывают:

· упругие (обратимые, т.е. исчезают после удаления причин их вызывающих);

· пластические (необратимые).

Гипотезы:

1. Гипотеза об отсутствии первоначальных внутренних усилий;

2. Принцип отвердевания (неизменность начальных размеров);

3. Гипотеза о линейных деформациях тел (закон Гука);

4. Принцип суперпозиции (независимость действия сил);

5. Гипотеза плоских сечений (плоские поперечные сечения бруса до деформации остаются плоскими и нормальными к оси бруса после деформации);

6. Принцип Сен-Венана.

· Внешними силами называют силы, которые выражают действия на тело других тел или внешней среды.

· Внутренними силами называется усилия или моменты, выражающие действия одной части на другую внутри какой-либо изолированной системы.

Внешние нагрузки (ВН) по характеру действия:

· статические;

· динамические (внезапно приложенные, ударные, циклические).

ВН по видам приложения:

·сосредоточенные;

·распределенные: (1) объемные;

(2) поверхностные;

(3) линейные.

ВН по возникновению:

· активные (силы, моменты);

· реактивные (реакции опор).

Опоры и опорные реакции

1)шарнирно-неподвижная опора 2)шарнирно-подвижная опора

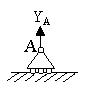
3)жесткая заделка

Внутренние силовые факторы (ВСФ), общий случай нагружений

где N – нормальная сила;

Q_x,Q_y – поперечные силы;

M_z – крутящий момент;

M_x,M_y – изгибающий момент.

Метод сечения – алгоритм из четырех действий. (Правило РОЗУ)

Р – разрезаем брус сечением, перпендикулярным его оси.

О – отбрасываем ту часть бруса, в которой больше всего неизвестных.

З – заменяем действия отброшенной части соответствующей равнодействующей.

У – уравновешиваем полученную систему (∑Fi=0; ∑Mi=0).

В теоретической механике доказана теорема Пуассона.

Теорема Пуассона:

Всякую систему сил относительно любой точки можно привести к эквивалентной системе, состоящей из главного вектора и главного момента, выходящих из этой точки.

Для того чтобы система находилась в состоянии равнодействия, необходимо и достаточно, чтобы главный вектор и главный момент были равны 0.

R_o=0 ; { R_ox=0; R_oy=0; R_oz=0 }

M_o=0; {M_ox=0; M_oy=0; M_oz=0}

Напряжением называется интенсивность внутренней силы в данной точке поперечного сечения (т.е. внутренняя сила, деленная на единицу площади). Аналог напряжения – давление.

1 Н/м²=1 Па

1 Н/мм²=1 МПа

Полным напряжением в точке называется отношение равнодействия сил к элементу имеющегося поперечного сечения.

где dF – площадь;

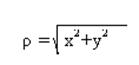
где ρ – полярный радиус (кратчайшее расстояние от точки приложения до центра тяжести)

dN/dF = σ

τ_x- касательное напряжение

τ_y- касательное напряжение

σ- нормальное напряжение

p= σ + τ_x + τ_y

Несложно установить зависимость между внутренними силовыми факторами и напряжением.

Замечание: Направление действия напряжения совпадает с направлением действия, вызывающих их сил.

· Абсолютная линейная деформация

- это разность между конечной и начальной длиной стержня.

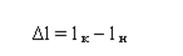
· Относительная линейная деформация

- это безразмерная величина, равная отношению абсолютной величины линейной деформации к первоначальной длине стержня.

· Абсолютная угловая деформация (абсолютный сдвиг)

- возникает при смещении двух параллельных плоскостей друг относительно друга под действием поперечных сил.

· Относительная угловая деформация (относительный сдвиг)

отношение абсолютной угловой деформации к расстоянию между сдвигающимися плоскостями:

Деформированное состояние точки тела полностью определяется

6-ю компонентами деформации:

Перемещенияявляются абсолютными величинами, выражаемыми в единицах длины или в радианах.

Деформации - относительные величины, выражаемые в процентах (безразмерные).

Центральное рстяжение-сжатие – такой вид деформации бруса, при котором в его поперечном сечении возникает только один внутренний силовой фактор отличный от 0 – нормальная (продольная) сила N, приложенная в центре тяжести поперечного сечения груза.

Если N действует от сечения, то она вызывает растяжение (увеличение длины) и считается положительной.

Если N действует к сечению, то она вызывает сжатие (укорочение бруса) и считается отрицательной.

N>0 – растяжение

N<0 – сжатие

Брусья, в основном работающие на растяжение-сжатие называются стержнями.

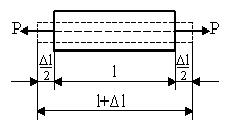
Экспериментально доказано:

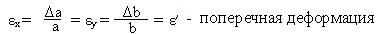
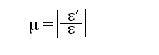При центральном растяжении–сжатии отношение поперечной деформации к продольной величине постоянно для данного материала и её абсолютное значение называется коэффицентом Пуассона.

0 ≤ μ ≤ 0,5 (в зависимости от пластичности)

Пример:

μ _пробки=0

μ_чугуна=0,23÷0,27

μ_стали=0,29÷0,33

μ_меди=0,31÷0,33

μ_{каучука}=0,47

Для большинства материалов с достаточной точностью можно сказать: