Парная линейная регрессия.
Линейное уравнение парной регрессии имеет вид:ŷ = b0 + b1 · x,где ŷ — оценка условного математического ожидания y; b0 , b1 — эмпирические коэффициенты регрессии, подлежащие определению. Рассмотрим в качестве примера зависимость между сменной добычей угля на одного рабочего Г(т) и мощностью пласта Дм) по следующим (условным) данным, характеризующим процесс добычи угля в п = 10 шахтах.
| i | ||||||||||
| xi | ||||||||||
| yi |
Полученная зависимость графически точками координатной плоскости. Такое изображение статистической зависимости называется полем корреляции. По расположению эмпирических точек можно предполагать наличие линейной корреляционной (регрессионной) зависимости между переменными Х и Y. Коэффициент bi называется выборочным коэффициентом регрессии (или просто коэффициентом регрессии) Y по X. Коэффициент регрессии У по X показывает, на сколько единиц в среднем изменяется переменная Y при увеличении переменной X на одну единицу.
Поэтому уравнение регрессии 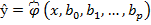 (3.2) будем искать в виде линейного уравнения: ŷ = b0 + b1(3.3). Согласно методу наименьших квадратовнеизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений ŷ, найденных по уравнению регрессии (3.3), была минимальной:
(3.2) будем искать в виде линейного уравнения: ŷ = b0 + b1(3.3). Согласно методу наименьших квадратовнеизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений эмпирических значений yi от значений ŷ, найденных по уравнению регрессии (3.3), была минимальной: 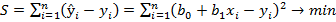 . (3.4) Для оценки параметров bo и b1 возможны и другие подходы. Например, согласно методу наименьших модулей следует минимизировать сумму абсолютных величин отклонений
. (3.4) Для оценки параметров bo и b1 возможны и другие подходы. Например, согласно методу наименьших модулей следует минимизировать сумму абсолютных величин отклонений  . Однако метод наименьших квадратов существенно проще.
. Однако метод наименьших квадратов существенно проще.
Средние величины находятся по формулам: 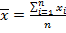 ;
;  ;
;  ;
; 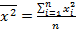 ; где n – кол-во. Уравнение регрессии будем искать в виде:
; где n – кол-во. Уравнение регрессии будем искать в виде:  . (3.12) Коэффициент b1 наз-ся выборочным коэффициентом регрессии или просто коэффициентом регрессии Y по X. Y по X. Показывает на сколько единиц в среднем изменяется переменная y при увеличении переменной x на 1.
. (3.12) Коэффициент b1 наз-ся выборочным коэффициентом регрессии или просто коэффициентом регрессии Y по X. Y по X. Показывает на сколько единиц в среднем изменяется переменная y при увеличении переменной x на 1.  , где cov – ковыряция, Sx2 – выборочная дисперсия переменной х; cov(x,y) – выборочная ковыряция.
, где cov – ковыряция, Sx2 – выборочная дисперсия переменной х; cov(x,y) – выборочная ковыряция.  .
.