Модель множеств регрессии.Выбор вида модели и оценка ее параметров.

Модель парной регрессии устанавливает зависимость интересующей нас величины только от 1-го фактора. На показатель влияет целая совокупность факторов. Если использовать линейную математическую функцию, то в этом случае модель множественной регрессии примет вид y_i=a₀+a₁x_i1+a₂x_i2+a₃x_i3+…+a_mx_im+e_i. Каждый из параметров модели а_i показывает, на сколько меняется исследуемая величина у при изменении соответствующего фактора на 1 единицу. Эта модель универсальна в том смысле, что позволяет установить зависимость показателя, как от всей совокупности факторов, так и от каждого из них в отдельности. Эта модель применяется при изучении проблем спроса, функции доходности акции, функции издержек производства, функции прибыли

Функция , описывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии. Уравнение регрессии показывает ожидаемое значение зависимой переменной при определенных значениях зависимых переменных .

В зависимости от количества включенных в модель факторов Х модели делятся на однофакторные (парная модель регрессии) и многофакторные (модель множественной регрессии).

В зависимости от вида функции модели делятся на линейные и нелинейные.

Модель множественной линейной регрессии имеет вид:

y _i = a₀ + a₁x _{i 1} +a₂x _{i 2} +…+ a_k x _{i k} + e_i (2.1)

- количество наблюдений.

коэффициент регрессии a_j показывает, на какую величину в среднем изменится результативный признак 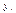, если переменную x_j увеличить на единицу измерения, т. е. a_j является нормативным коэффициентом.

Коэффициент может быть отрицательным. Это означает, что область существования показателя не включает нулевых значений параметров. Если же а0>0, то область существования показателя включает нулевые значения параметров, а сам коэффициент характеризует среднее значение показателя при отсутствии воздействий параметров.

Анализ уравнения (2.1) и методика определения параметров становятся более наглядными, а расчетные процедуры существенно упрощаются, если воспользоваться матричной формой записи:

(2.2) .

Где У – вектор зависимой переменной размерности п ´ 1, представляющий собой п наблюдений значений .

Х- матрица п наблюдений независимых переменных 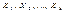, размерность матрицы Х равна п ´ (k+1) . Дополнительный факторХ0, состоящий из единиц, вводится для вычисления свободного члена. В качестве исходных данных могут быть временные ряды или пространственная выборка.

К - количество факторов, включенных в модель.

a— подлежащий оцениванию вектор неизвестных параметров размерности (k+1) ´ 1;

— вектор случайных отклонений (возмущений) размерности п ´ 1. отражает тот факт, что изменение будет неточно описываться изменением объясняющих переменных , так как существуют и другие факторы, неучтенные в данной модели.

Таким образом,

Y = ,

X = , ,

a = .

 

Уравнение (2.2) содержит значения неизвестных пара­метров a₀,a₁,a₂,… ,a_k

Эти величины оцениваются на основе выборочных наблюдений, поэтому полученные расчетные показатели не являются истинными, а представляют собой лишь их статистические оценки. Модель линейной регрес­сии, в которой вместо истинных значений параметров под­ставлены их оценки (а именно такие регрессии и приме­няются на практике), имеет вид

, (2.3)

где A— вектор оценок параметров; е — вектор «оценен­ных» отклонений регрессии, остатки регрессии е = Y - ХА; —оценка значе­ний Y, равнаяХА.