Дифференциал функции

Можно доказать, что если функция имеет при некоторой базе предел, равный конечному числу, то ее можно представить в виде суммы этого числа и бесконечно малой величины при той же базе (и наоборот): .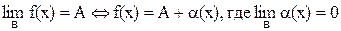

Применим это теорему к дифференцируемой функции: .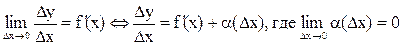

Отсюда .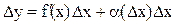

Таким образом, приращение функции Dу состоит из двух слагаемых: 1) линейного относительно Dх, т.е. f `(x)Dх; 2) нелинейного относительно Dх, т.е. a(Dx)Dх. При этом, так как 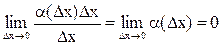, это второе слагаемое представляет собой бесконечно малую более высокого порядка, чем Dх (при стремлении Dх к нулю оно стремится к нулю еще быстрее).

 

Дифференциалом функции называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной dy = f `(x)Dх.

 

Найдем дифференциал функции у = х.

Так как dy = f `(x)Dх = x`Dх = Dх, то dx = Dх, т.е. дифференциал независимой переменной равен приращению этой переменной.

Поэтому формулу для дифференциала функции можно записать в виде dy = f `(x)dх. Именно поэтому одно из обозначений производной представляет собой дробь dy/dх.

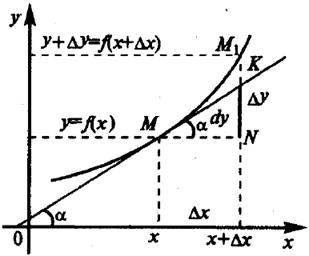
Геометрический смысл дифференциала проиллюстрирован
рисунком 3.11. Возьмем на графике функции y = f(x) произвольную точку М(х, у). Дадим аргументу х приращение Dх. Тогда функция y = f(x) получит приращение Dy = f(x + Dх) - f(x). Проведем касательную к графику функции в точке М, которая образует угол a с положительным направлением оси абсцисс, т.е. f `(x) = tg a. Из прямоугольного треугольника MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.

Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение Dх.

 

Свойства дифференциала в основном аналогичны свойствам производной:

1. dc = 0.

2. d(cu)=c du.

3. d(u ± v) = du ± dv.

4. d(uv) = v du + u dv.

5. d(u/v) = (v du - u dv)/v².

Однако, существует важное свойство дифференциала функции, которым не обладает ее производная – это инвариантность формы дифференциала.

Из определения дифференциала для функции y = f(x) дифференциал dy = f `(x)dх. Если эта функция y является сложной, т.е. y = f(u), где u = j(х), то y = f[j(х)] и f `(x) = f `(u)*u`. Тогда dy = f `(u)*u`dх. Но для функции
u = j(х) дифференциал du = u`dх. Отсюда dy = f `(u)*du.

Сравнивая между собой равенства dy = f `(x)dх и dy = f `(u)*du, убедимся, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной u. Это свойство дифференциала и получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.

Однако в этих двух формулах все же есть различие: в первой из них дифференциал независимой переменной равен приращению этой переменной, т.е. dx = Dx, а во в торой дифференциал функции du есть лишь линейная часть приращения этой функции Du и только при малых Dх du » Du.