Структура сети Вольтерри
Сеть Вольтерри
Сеть Вольтерри относится к сетям со специализированной структурой. Это динамическая сеть для нелинейной обработки последовательности сигналов, задержанных относительно друг друга. Возбуждением для сети в момент  служит вектор
служит вектор 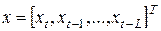 , где
, где  - количество единичных задержек, а
- количество единичных задержек, а 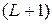 означает длину вектора. В соответствии с определением ряда Вольтерри выходной сигнал
означает длину вектора. В соответствии с определением ряда Вольтерри выходной сигнал 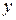 генерируется по формуле:
генерируется по формуле:
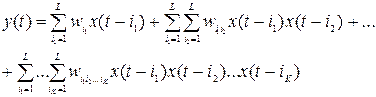 (7.1)
(7.1)
где  обозначает входной сигнал, а веса
обозначает входной сигнал, а веса 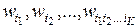 , называемые ядрами Вольтерри, соответствуют реакциям высших порядков. Порядок полинома Вольтерри
, называемые ядрами Вольтерри, соответствуют реакциям высших порядков. Порядок полинома Вольтерри  также называется степенью ряда Вольтерри.
также называется степенью ряда Вольтерри.
Нелинейная функциональная зависимость Вольтерри является полиномиальным обобщением описания линейного фильтра FIR. Порядок этого полинома K называется степенью ряда Вольтерри. Пусть целевая функция для одного обучающего вектора выражается формулой:
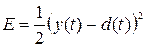 (7.2)
(7.2)
В этом случае можно минимизировать значение целевой функции градиентными методами, которые сводятся к решению системы дифференциальных уравнений вида:
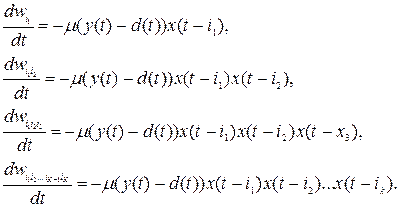 (7.3)
(7.3)
Для упрощения структуры сети представленное разложение Вольтерри можно записать в следующей форме:
 , (7.4)
, (7.4)
где используются обозначения  и т.д. Каждое слагаемое в квадратных скобках представляет собой линейный фильтр первого порядка, в котором соответствующие веса представляют импульсную реакцию другого линейного фильтра следующего уровня. Количество уровней, на которых создаются фильтры, равно порядку
и т.д. Каждое слагаемое в квадратных скобках представляет собой линейный фильтр первого порядка, в котором соответствующие веса представляют импульсную реакцию другого линейного фильтра следующего уровня. Количество уровней, на которых создаются фильтры, равно порядку  . На рисунке 7.1 показано распространение сигналов по сети Вольтерри, реализующей зависимость (7.4) при ограничении
. На рисунке 7.1 показано распространение сигналов по сети Вольтерри, реализующей зависимость (7.4) при ограничении 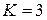 .
.
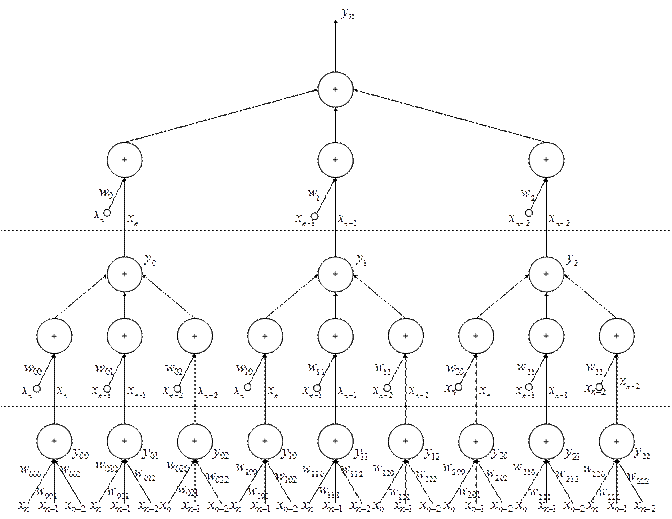
Рисунок 7.1 – Граф сети Вольтерри
Система представляет собой структуру типичной многослойной однонаправленной динамической нейронной сети. Это сеть с полиномиальной нелинейностью. Подбор весов производится последовательно слой за слоем, причём эти процессы независимы друг от друга, и, увеличение числа весов в слое и числа самих слоёв в незначительной степени сказывается на обусловленности задачи. Это даёт возможность существенно увеличить длину  и порядок
и порядок  системы при её практической реализации. Обучение нейронной сети Вольтерри лучше всего приводить с использованием технологии сопряжённых графов.
системы при её практической реализации. Обучение нейронной сети Вольтерри лучше всего приводить с использованием технологии сопряжённых графов.
Для сети, представленной на рисунке 7.1, сопряжённый граф строится без особого труда (рисунок 7.2).
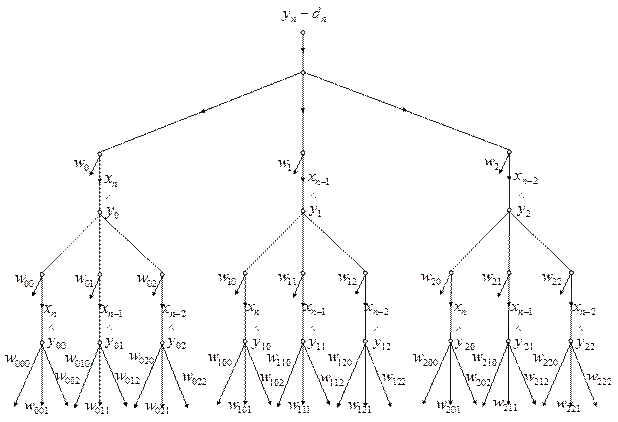
Рисунок 7.2 – Сопряженный граф сети Вольтерри
В соответствии с обозначениями, принятыми на рисунках, возбуждением сопряженного графа служит разностный сигнал  , где
, где  обозначает ожидаемое, а
обозначает ожидаемое, а 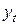 - фактическое значение в выходном узле системы в момент
- фактическое значение в выходном узле системы в момент  . Формулы для определения конкретных компонентов вектора градиента имеют вид:
. Формулы для определения конкретных компонентов вектора градиента имеют вид:
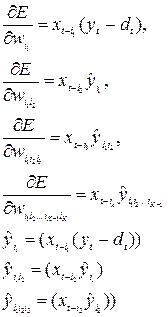 (7.5)
(7.5)
В приведенных формулах сигналы, обозначенные символом ^, соответствуют сопряженному, а остальные – исходному графу системы. После определения конкретных компонентов градиента обучение сети с применением оптимизационного метода наискорейшего спуска может быть сведено к решению дифференциальных уравнений:
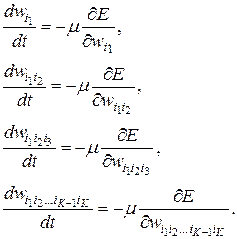 (7.6)
(7.6)
где 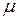 - коэффициент обучения.
- коэффициент обучения.
Важным достоинством метода сопряженных графов считается простота учета равных значений весов в различных ветвях сети. Симметрия ядер Вольтерри приводит к равенству весов  для всех перестановок индексов
для всех перестановок индексов  . Для двухиндексных весов это означает, что
. Для двухиндексных весов это означает, что 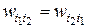 . Подобные соотношения можно написать и для трёхиндексных и четырёхиндексных и так далее весов. Анализ обозначений весов сети, изображённой на рисунке 7.1, позволяет найти веса, которые имеют одни и те же значения.
. Подобные соотношения можно написать и для трёхиндексных и четырёхиндексных и так далее весов. Анализ обозначений весов сети, изображённой на рисунке 7.1, позволяет найти веса, которые имеют одни и те же значения.
С учетом симметрии ядер Вольтерри выражения, описывающие компоненты градиента относительно весов  , могут быть определенным образом модифицированы:
, могут быть определенным образом модифицированы:
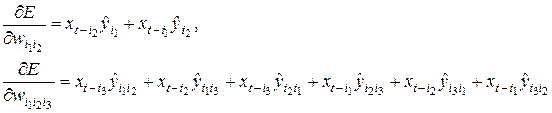 (7.7).
(7.7).