Модель МакКаллока - Питса

Из приведенных выше рассуждений следует, что каждый нейрон суммирует с соответствующими весами сигналы, приходящие от других нейронов, выполняет нелинейную решающую функцию и передает результат связанным с ним другим нейронам. В простейших моделях нейронов выходной сигнал принимает двоичные значения: 0 или 1. Значение 1 соответствует превышению порогового уровня, значение 0 – в противном случае. Одна из первых моделей нейрона была предложена Дж. МакКаллоком и У. Питсом в 1943 году [5]. Структурная схема этой модели представлена на рис. 2.5.

Сигналы x_j на входе синапсов j (j = 1,2,…,N), связанные с нейроном i, суммируются с учетом соответствующих синаптических весов w_ij (первый индекс относится к нейрону, а второй к синапсу), после чего результат сравнивается с пороговым значением w_i0 . Пороговое значение отражает увеличение или уменьшение входного сигнала, подаваемого на функцию активации. Выходной сигнал нейрона y_i определяется при этом зависимостью

(2.1)

 

 

 

Рис. 2.5 Модель нейрона МакКаллока-Питса

 

Аргументом функции выступает суммарный сигнал

. (2.2)

Коэффициенты 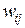в формуле (2.1) представляют веса синапсов. Положительные значения 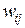соответствует синапсам, повышающим потенциал, отрицательные значения – синапсам, понижающим потенциал, свидетельствует об отсутствии связи между i-м и j-м нейронами.

Модель МакКаллока – Питса – это дискретная модель, в которой состояние нейрона в момент (t+1) рассчитывается по значению его входных сигналов в момент времени t.

Функция f(u_i) называется функцией активации. В модели МакКаллока – Питса это пороговая функция вида:

. (2.3)

В общем случае эта функция активации описывается следующим выражением:

(2.4)

где b и c – некоторые постоянные. На практике чаще всего используют две пары постоянных b и c: первая (-1,1); вторая – (0,1). Первая пара коэффициентов определяет так называемую симметричную пороговую функцию, вторая – смещенную.