Технология решения задач корреляционного и регрессионного анализа с помощью пакета анализа.
Пакет анализа - это надстройка, которая представляет широкие возможности для проведения статистического анализа.
Установка средств Пакет анализа.
В стандартной конфигурации программы EXCEL вы не найдете средства Пакет анализа. Даже если установить их с компакт-диска EXCEL'97 (или Office'97), они не появятся в меню до тех пор, пока вы не установите их в качестве надстройки Excel. Для этого выполните следующие действия:
1. Выберите команду Сервис=>Надстройки.
2. В диалоговом окне Надстройки установите флажок Пакет анализа.
3. Щелкните на кнопке ОК.
После этого в нижней части меню Сервис появится новая команда Анализ данных. Эта команда предоставляет доступ к средствам анализа, которые есть в EXCEL.
Пример 2.2.1. Задача состоит в построении модели для предсказания объема реализации одного из продуктов фирмы.
Объем реализации - это зависимая переменная Y. В качестве независимых, объясняющих переменных выбраны: время – Х1, расходы на рекламу Х2, цена товара Х3, средняя цена конкурентов X4, индекс потребительских расходовX5.
1. Построение системы показателей (факторов). Анализ матрицы коэффициентов парной корреляции
Статистические данные по всем переменным приведены в табл. 2.2.1. В этом примере n = 16, m = 5.
Таблица 2.2.1
| Y | XI | XI | X3 | Х4 | Х5 |
| объем реализации | время | реклама | цена | цена конкурента | индекс потребительских расходов |
| 4,8 | 14.8 | 17.3 | 98.4 | ||
| 3.8 | 15.2 | 16.8 | 101.2 | ||
| 8.7 | 15.5 | 16.2 | 103.5 | ||
| 8.2 | 15.5 | 104.1 | |||
| 9.7 | |||||
| 14.7 | 18.1 | 20.2 | 107.4 | ||
| 18.7 | 15.8 | 108.5 | |||
| 19.8 | 15.8 | 18.2 | 108.3 | ||
| 10.6 | 16.9 | 16.8 | 109.2 | ||
| 8.6 | 16.3 | 110.1 | |||
| 6.5 | 16.1 | 18.3 | 110.7 | ||
| 12.6 | 15.4 | 16.4 | 110.3 | ||
| 6.5 | 15.7 | 16.2 | 111.8 | ||
| 5.8 | 17.7 | 112.3 | |||
| 5.7 | 15.1 | 16.2 | 112.9 |
Использование инструментаКорреляция. Для проведения корреляционного анализа выполните следующие действия:
1) данные для корреляционного анализа должны располагаться в смежных диапазонах ячеек;
2) выберите команду Сервис =>Анализ данных;
3) в диалоговом окне Анализ данных выберите инструмент Корреляция (рис. 4.2.1). а затем щелкните на кнопке ОК;
4) в диалоговом окне Корреляция в поле «Входной интервал» необходимо ввести диапазон ячеек, содержащих исходные данные. Если выделены и заголовки столбцов, то установить флажок «Метки в первой строке» (рис. 4.2.2);
5) выберите параметры вывода. В данном примере - установите переключатель «Новый рабочий лист»;
6) ОК.
В табл. 2.2.2 приведены промежуточные результаты при вычислении коэффициента корреляции по формуле (2.1.1)
Таблица 2.2.2
| t | Y | X2 | 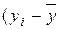 ) )
| 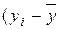 )2 )2
| 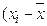 ) )
| 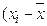 )2 )2
| 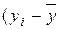 )× )× 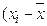 ) )
|
| 4.8 | -180.813 -169.813 | 32693.16 28836.29 | -5.29375 -4.49375 | 28.02379 20.19379 | 957.1762 763.0949 | ||
| 3.8 | -158.813 | 25221.41 | -5.49375 | 30.18129 | 872.4762 | ||
| 8.7 | -115.813 | 13412.54 | -0.59375 | 0.352539 | 68.76367 | ||
| 8.2 | -32.8125 | 1076.66 | -1.09375 | 1.196289 | 35.88867 | ||
| 9.7 | 63.1875 | 3992.66 | 0.40625 | 0.165039 | 25.66992 | ||
| 14.7 | 125.1875 | 15671.91 | 5.40625 | 29.22754 | 676.7949 | ||
| 18.7 | 138.1875 | 19095.79 | 9.40625 | 88.47754 | 1299.826 | ||
| 19.8 | 60.1875 | 3622.535 | 10.50625 | 110.3813 | 632.3449 | ||
| 10.6 | 60.1875 | 3622.535 | 1.30625 | 1.706289 | 78.61992 | ||
| 8.6 | 14.1875 | 201.2852 | -0.69375 | 0.481289 | -9.84258 | ||
| 6.5 | 0.1875 | 0.035156 | -2.79375 | 7.805039 | -0.52383 | ||
| 12.6 | 24.1875 | 585.0352 | 3.30625 | 10.93129 | 79.96992 | ||
| 6.5 | 38.1875 | 1458.285 | -2.79375 | 7.805039 | -106.686 | ||
| 5.8 | 57.1875 | 3270.41 | -3.49375 | 12.20629 | -199.799 | ||
| 5.7 | 77.1875 | 5957.91 | -3.59375 | 12.91504 | -277.393 | ||
| Сумма | 148.7 | 158718.4 | 362.0494 | 4896.381 | |||
| Среднее значение | 306.8125 | 9.29375 |
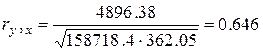
Таблица 2.2.3
| Объем реализации | Время | Реклама | Цена | Цена конкурента | Индекс потребительских расходов | |
| Столбец 1 | Столбец 2 | Столбец З | Столбец 4 | Столбец 5 | Столбец 6 | |
| Объем реализации | ||||||
| Время Реклама | 0.678 0.646 | 1 0.106 | ||||
| Цена | 0.233 | 0.174 | -0.003 | |||
| Цена конкурента | 0.226 | -0.051 | 0.204 | 0.698 | ||
| Индекс отребительских расходов | 0.816 | 0.960 | 0.273 | 0.235 | 0.030 |
Анализ матрицы коэффициентов парной корреляции (табл. 2.2.3) показывает, что зависимая переменная, т.е. объем реализации, имеет тесную связь с индексом потребительских расходов (ryx5 = 0.816), с расходами на рекламу (ryx5=0.646) и со временем (ryx1 =0.678). Однако факторы X2; и X5 тесно связаны между собой (ryx5= 0.96), что свидетельствует о наличии мультиколлинеарности. Из этих двух переменных оставим в модели X5 - индекс потребительских расходов. В этом примере n= 16, m = 5, после исключения незначимых факторов п = 16, k = 2.
2. Выбор вида модели и оценка ее параметров
Оценка параметров регрессии осуществляется по методу наименьших квадратов по формуле (2.1.6), с использованием данных, приведенных в табл. 2.2.4.
Таблица 2.2.4
| y | X0 | X1 | X2 |
| объем реализации | реклама | индекс потребительских расходов | |
| 4.8 | 98.4 | ||
| 3.8 | 101.2 | ||
| 8.7 | 103.5 | ||
| 8.2 | 104.1 | ||
| 9.7 | |||
| 14.7 | 107.4 | ||
| 18.7 | 108.5 | ||
| 19.8 | 108.3 | ||
| 10.6 | 109.2 | ||
| 8.6 | 110.1 | ||
| 6.5 | 110.7 | ||
| 12.6 | 110.3 | ||
| 6.5 | 111.8 | ||
| 5.8 | 112.3 | ||
| 5.7 | 112.9 |
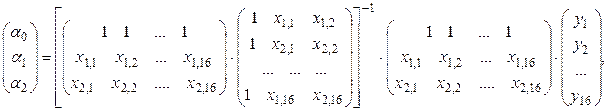
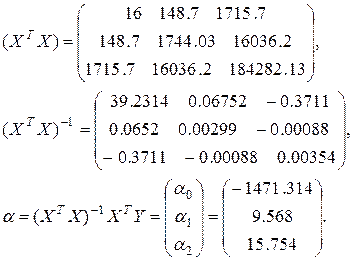
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов можно записать в следующем виде:
Y= -1471.314 + 9.568Х1 + 15.754Х2.
Расчетные значения Y определяются путем последовательной подстановки в эту модель значений факторов, взятых для каждого момента времени t.
return false">ссылка скрытаПрименение инструмента Регрессия. Для проведения регрессионного анализа выполните следующие действия:
1) выберите команду Сервис ÞАнализ данных;
2) в диалоговом окне Анализ данных выберите инструмент Регрессия, а затем щелкните на кнопке ОК;
3) в диалоговом окне Регрессия в поле «Входной интервал Y» введите адрес одного диапазона ячеек, который представляет зависимую переменную. В поле «Входной интервал X» введите адреса одного или нескольких диапазонов, которые содержат значения независимых переменных;
4) если выделены и заголовки столбцов, то установить флажок Метки в первой строке;
5) выберите параметры вывода. В данном примере - установите переключатель «Новая рабочая книга»',
6) в поле «Остатки» поставьте необходимые флажки;
7) ОК.
Таблица 2.2.5
| Регрессионная статистика | |
| Множественный R R- квадрат Нормированный R-квадрат Стандартная ошибка Наблюдения | 0.927 0.859 0.837 41.473 16.000 |
Пояснения к табл. 2.2.5.
| Регрессионная статистика | |||
| № | Наименование в отчете EXCEL | Принятые наименования | Формула |
| Множественный R | Коэффициент множественной корреляции, индекс корреляции | 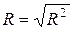
| |
| R-квадрат | Коэффициент детерминации, R2 | 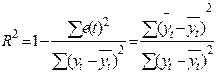
| |
| Нормированный R-квадрат | Скорректированный R2 | 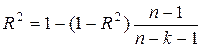
| |
| Стандартная ошибка | Стандартная ошибка оценки | 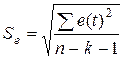
| |
| Наблюдения | Количество наблюдений, n | n |
Таблица 2.2.6
| Дисперсионный анализ | ||||
| Df | SS | MS | F | |
| Регрессия Остаток Итого | 136358.334 22360.104 158718.438 | 68179.167 1720.008 | 39.639 |
Пояснения к табл. 2.2.6.
| Df- число степеней свободы | SS - сумма квадратов | MS | F - критерий Фишера | |
| Регрессия | k=2 | 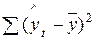
| 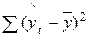 /k /k
| 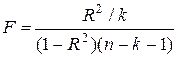
|
| Остаток | n-k-1=l3 | 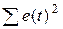
| 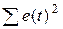 /(n-k-1) /(n-k-1)
| |
| Итого | n-1 =15 | 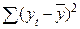
|
Таблица 2.2.7
| Коэффициенты | Стандартная ошибка | t-статистика | |
| Y-пересечение Реклама Индекс потребительских расходов | -1471.3143 9.5684 15,7529 | • 259.7660 2.2659 2.4669 | -5.6640 4.2227 6.3858 |
Во втором столбце табл. 2.2.7 содержатся коэффициенты уравнения регрессии a0, a1, a2. В третьем столбце содержатся стандартные ошибки коэффициентов уравнения регрессии (2.1.12), а в четвертом - г-статистика (2.1.11), используемая для проверки значимости коэффициентов уравнения регрессии.
Уравнение регрессии зависимости объема реализации от затрат на рекламу и индекса потребительских расходов, полученное с помощью EXCEL, как было указано ранее, имеет вид:
Y =-1471.314+9.568Х1.+15.754Х2.
Таблица 2.2.8
| ВЫВОД ОСТАТКА | ||||
| Наблюдение | Предсказанное Y | Остатки | ||
| 142.247 | -16.247 | |||
| 124.697 | 12.303 | |||
| 159.237 | -11.237 | |||
| 242.353 | -51.353 | |||
| 247.021 | 26.979 | |||
| 307.057 | 62.943 | |||
| 361.200 | 70.800 | |||
| 416.802 | 28.198 | |||
| 424.177 | -57.177 | |||
| 350.325 | 16.675 | |||
| 345.365 | -24.365 | |||
| 334.724 | -27.724 | |||
| 386.790 | -55.790 | |||
| 352.052 | -7.052 | |||
| 353.230 | 10.770 | |||
| 361.725 | 22.275 | |||
3. Оценка качества модели
В табл. 2.2.8 приведены вычисленные по модели значения Y и значения остаточной компоненты.
Проверку независимости проведем с помощью rf-критерия Дарбина-Уотсона.
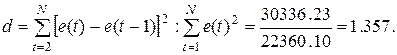
В качестве критических табличных уровней при N = 16, двух объясняющих факторах при уровне значимости 5% возьмем величины d1 =0,98 и d2 = 1,54.
Так как расчетное значение попало в интервал от d1 до d2, то нельзя сделать окончательный вывод по этому критерию. Для определения степени автокорреляции вычислим коэффициент автокорреляции и проверим его значимость при помощи критерия стандартной ошибки.
Стандартная ошибка коэффициента корреляции рассчитывается следующим образом:

Коэффициенты автокорреляции случайных данных обладают выборочным распределением, приближающимся к нормальному с нулевым математическим ожиданием и средним квадратическим отклонением, равным 
Если r1находится в интервале:
-0,96×0.25£r1 £1.96×0.25,
то можно считать, что данные не показывают наличие автокорреляции первого порядка, так как
-0.49£ r1 =0.305£0.49,
и свойство независимости выполняется.
Вычислить для модели коэффициент детерминации
 =
=
=1-22360.104/158718.44=136358.3/158718.44=0.859.
Он показывает долю вариации результативного признака под воздействием изучаемых факторов. Следовательно, около 86% вариации зависимой переменной учтено в модели и обусловлено влиянием включенных факторов.
Проверку значимости уравнения регрессии произведем на основе вычисления F-критерия Фишера:

Табличное значение F-критерия при доверительной вероятности 0,95v1=k=2 и v2 =n-k- 1 = 16-2- 1 = 13 составляет 4.81.
Поскольку Fрас > Fтабл. уравнение регрессии следует признать адекватным.
Значимость коэффициентов уравнения регрессии a1, a2 оценим с использованием t-критерия Стьюдента.


b22=0.00299,
b33=0.00354,

Табличное значение /-критерия при уровне значимости 5% и степенях свободы (16-2-1=13) составляет 1,77. Так как tpac> tтабл, то коэффициенты a1, a2 существенны (значимы).
4. Проанализировать влияние факторов на зависимую переменную по модели (для каждого коэффициента регрессии вычислить коэффициент эластичности, b-коэффициент)
Учитывая, что коэффициент регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, используем коэффициент эластичности (Э) и b -коэффициент, которые соответственно рассчитываются по формулам:
Эi = аi × Xср: Ycр;
Э1 =9.568-9.294/306.813= 0.2898;
Э2=15.7529- 107.231 /306.813=5.506;
bi; = , ai× Sxi : Sy,
где 
b1=9.568-4.913/ 102.865=0.457;
b2= 15.7529-4.5128/ 102.865=0.691.
Коэффициент эластичности показывает, на сколько процентов изменяется зависимая переменная при изменении фактора на 1%.
Бета-коэффициент с математической точки зрения показывает, на какую часть величины среднего квадратического отклонения меняется среднее значение зависимой переменной с изменением независимой переменной на одно среднее квадратическое отклонение при фиксированном на постоянном уровне значении остальных независимых переменных. Это означает, что при увеличении затрат на рекламу в нашем примере на 4.91 тыс. руб. объем реализации увеличится на 47 тыс. руб. (0.457-102.865).
5. Определить точечные и интервальные прогнозные оценки объема реализации на два квартала вперед (t0.7=1.12)
Прогнозные значения X1np(17), X2пр(18) и Х1np(17), X2пр(18) можно определить или вычислить на основе экстраполяционных методов.
Для фактора Х\ Затраты на рекламу выбрана модель
X1 = 12.83 - 11.616t + 4.319t2 - 0.552t3 + 0.020t4 - О.ООО6t5,по которой получен прогноз на два месяца вперед'. Графики модели временного ряда Затраты на рекламу приведены на рис. 2.2.6.
| Упреждение | Прогноз |
| 5,75 | |
| 4,85 |
Для временного ряда Индекс потребительских расходов в качестве аппроксимирующей функции выбран полином второй степени (парабола), по которой построен прогноз на два шага вперед. Индекс потребительских расходов
Х2 = 97.008 +1.739 t- 0.0488 t2.
| Упреждение | Прогноз |
| 112.468 | |
| 112.488 |
Для получения прогнозных оценок зависимостей переменной по модели Y = -1471.438 + 9.568Х1 + 15.754 Х2 подставим в нее найденные прогнозные значения факторовХ1 и Х2.
Y1=17 = -1471.438 + 9.568 • 5.75 + 15.754 • 112.468 = 355.399,
Yt=18„i8=-1471.438+9.568-4.85 + 15.754- 112.488=344.179.
Доверительный интервал прогноза будет иметь следующие границы:
Верхняя граница прогноза: Yпр (N + 1) + U(l),
Нижняя граница прогноза: Ynp(N+ 1) - U(l),

Se=41.473, tкр=2,16*, l=1,  U(2)=45.749.
U(2)=45.749.
Результаты прогнозных оценок модели регрессии представим в таблице прогнозов (р =95%), табл. 2.2.9.
Таблица 2.2.9
| Упреждение | Прогноз | Нижняя граница | Верхняя граница |
| 355.399 | 312.368 | 398.367 | |
| 344.179 | 298.43 | 389 928 |
Задача 1.
Имеются данные о деятельности крупнейших компаний США в (2.2.10).
Таблица 2.2.10
| № п\п | Чистый доход, млрд. долл. США., у | Оборот капитала, млрд. долл. США,Х1 | Использованный капитал, млрд. долл. США, x2 | Численность служащих, тыс. чел., x3 | Рыночная капитализация компании, млрд. долл. США,Х4 |
| 0,9 | 31,3 | 18,9 | 43,0 | 40,9 | |
| 1,7 | 13,4 | 13,7 | 64,7 | 40,5 | |
| 0,7 | 4,5 | 18,5 | 24,0 | 38,9 | |
| 1,7 | 10,0 | 4,8 | 50,2 | 38,5 | |
| 2,6 | 20,0 | 21,8 | 106,0 | 37,3 | |
| 1,3 | 15,0 | 5,8 | 96,6 | 26,5 | |
| 4,1 | 137,1 | 99,0 | 347,0 | 37,0 | |
| 1,6 | 17,9 | 20,1 | 85,6 | 36,8 | |
| 9 | 6,9 | 165,4 | 60,6 | 745,0 | 36,3 |
| 0,4 | 2,0 | 1,4 | 4,1 | 35,3 | |
| 1,3 | 6,8 | 8,0 | 26,8 | 35,3 | |
| 1,9 | 27,1 | 18,9 | 42,7 | 35,0 | |
| 1,9 | 13,4 | 13,2 | 61,8 | 26,2 | |
| 1,4 | 9,8 | 12,6 | 212,0 | 33,1 | |
| 0,4 | 19,5 | 12,2 | 105,0 | 32,7 | |
| 0,8 | 6,8 | 3,2 | 33,5 | 32,1 | |
| 1,8 | 27,0 | 13,0 | 142,0 | 30,5 | |
| 0,9 | 12,4 | 6,9 | 96,0 | 29,8 | |
| 1,1 | 17,7 | 15,0 | 140,0 | 25,4 | |
| 1,9 | 12,7 | 11,9 | 59,3 | 29,3 | |
| -0,9 | 21,4 | 1,6 | 131,0 | 29,2 | |
| 1,3 | 13,5 | 8,6 | 70,7 | 29,2 | |
| 2,0 | 13,4 | 11,5 | 65,4 | 29,1 | |
| 0,6 | 4,2 | 1,9 | 23,1 | 27,9 | |
| 0,7 | 15,5 | 5,8 | 80,8 | 27,2 |
Задание
1. Рассчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
2. Дайте сравнительную оценку силы связи факторов с результатом с помощью средних (общих) коэффициентов эластичности.
3. Оцените статистическую значимость параметров регрессионной модели с помощью г-критерия; нулевую гипотезу о значимости уравнения и показателей тесноты связи проверьте с помощью F-критерия.
4. Оцените качество уравнения через среднюю ошибку аппроксимации.
5. Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе и по г-критерию для коэффициентов регрессии отберите информативные факторы в модель. Постройте модель только с информативными факторами и оцените ее параметры.
6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
7. Рассчитайте ошибки и доверительный интервал прогноза для уровня значимости 5 или 10% (а = 0,05; а = 0,10).
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Задача 2.
Имеются данные о деятельности крупнейших компаний США в 1996 г. (табл. 2.2.11).
Таблица 2.2.11
| № п/п | Чистый доход, млрд. долл. США, у | Оборот капитала, млрд. долл. США, хi | Использованный капитал, млрд. долл. США, xi | Численность служащих, тыс. чел., х3 |
| 6,6 | 6,9 | 83,6 | 222,0 | |
| 3,0 | 18,0 | 6,5 | 32,0 | |
| 6,5 | 107,9 | 50,4 | 82,0 | |
| 3,3 | 16,7 | 15,4 | 45,2 | |
| 0,1 | 79,6 | 29,0 | 299,3 | |
| 3,6 | 16,2 | 13,3 | 41,6 | |
| 1,5 | 5,9 | 5.9 | 17,8 | |
| 5,5 | 53,1 | 27,1 | 151,0 | |
| 9 | 2,4 | 18,8 | 11,2 | 82,3 |
| 3,0 | 35,3 | 16,4 | 103,0, | |
| 4,2 | 71,9 | 32,5 | 225,4 | |
| 2,7 | 93,6 | 25,4 | 675,0- | |
| 1,6 | 10,0 | 6,4 | 43,8 | |
| 2,4 | 31,5 | 12,5 | 102,3 | |
| 3,3 | 36,7 | 14,3 | 1б5,0 | |
| 1,8 | 13,8 | 6,5 | 49,1 | |
| 2,4 | 64,8 | 22,7 | 50,4 | |
| 1,5 | 30,4 | 15,8 | 480,0 | |
| 1,4 | 12,1 | 9,3 | 71,0 | |
| 0,9 | 31,3 | 18,9 | 43,0 |
1. Расчитайте параметры линейного уравнения множественной регрессии с полным перечнем факторов.
2. Дайте сравнительную оценку силы связи факторов с результатом с > средних (общих) коэффициентов эластичности.
3. Оцените статистическую значимость параметров регрессионной помощью г-критерия; нулевую гипотезу о значимости 1 и показателей тесноты связи проверьте с помощью F-критерия
4. Оцените качество уравнения через среднюю ошибку аппроксимации.
5. Рассчитайте матрицы парных и частных коэффициентов корреляции и на их основе и по t-критерию для коэффициентов регрессии отберите информативные факторы в модель. Постройте модель, информативными факторами и оцените ее параметры.
6. Рассчитайте прогнозное значение результата, если прогнозные значения факторов составляют 80% от их максимальных значений.
7. Рассчитайте ошибки и доверительный интервал прогноза для уравнения значимости 5 или 10% (а = 0,05; а = 0,10).
8. Оцените полученные результаты, выводы оформите в аналитической.
Задача 3
В табл. 2.2.12 представлены данные о рынке строящегося жилья в Санкт-Петербурге (по состоянию на декабрь 1996 г.).
| № п/п | X1 | X2 | X3 | Х4 | X5 | X6 | X7 | X8 | У |
| 39,0 | 20,0 | 8,2 | 15,9 | ||||||
| 68,4 | 40,5 | 10,7 | 27,0 | ||||||
| 34,8 | 16,0 | 10,7 | 13,5 | ||||||
| 39,0 | 20,0 | 8,5 | 15,1 | ||||||
| 54,7 | 28,0 | 10,7 | 21,1 | ||||||
| 74,7 | 46,3 | 10,7 | 28,7 | ||||||
| 71,7 | 45,9 | 10,7 | 27,2 | ||||||
| 74,5 | 47,5 | 10,4 | 28,3 | ||||||
| 137,7 | 87,2 | 14,6 | 52,3 | ||||||
| 40,0 | 17,7 | 11,0 | 22,0 | ||||||
| 53,0 | 31,1 | 10,0 | 28,0 | ||||||
| 86,0 | 48,7 | 14,0 | 45,0 | ||||||
| 98,0 | 65,8 | 13,0 | 51,0 | ||||||
| 2 | 62,6 | 21,4 | 11,0 | 34,4 | |||||
| 45,3 | 20,6 | 10,4 | 24,7 | ||||||
| 56,4 | 29,7 | 9,4 | 30,8 | ||||||
| 37,0 | 17,8 | 8,3 | 15,9 | ||||||
| 67,5 | 43,5 | 8,3 | 29,0 | ||||||
| 37,0 | 17,8 | 8,3 | 15,4 | ||||||
| 69,0 | 42,4 | 8,3 | 28,6 | ||||||
| 40,0 | 20,0 | 8,3 | 15,6 | ||||||
| 69,1 | 41,3 | 8,3 | 27,7 | ||||||
| 68,1 | 35,4 | 13,0 | 34,1 | ||||||
| 75,3 | 41,4 | 12,1 | 37,7 | ||||||
| 83,7 | 48,5 | 12,1 | 41,9 | ||||||
| 48,7 | 22,3 | 12,4 | 24,4 | ||||||
| 39,9 | 18,0 | 8,1 | 21,3 | ||||||
| 68,6 | 35,5 | 17,0 | 36,7 | ||||||
| 39,0 | 20,0 | 9,2 | 21,5 | ||||||
| 48,6 | 31,0 | 8,0 | 26,4 | ||||||
| 98,0 | 56,0 | 22,0 | 53,9 | ||||||
| 68,5 | 30,7 | 8,3 | 34,2 | ||||||
| 71,1 | 36,2 | 13,3 | 35,6 | ||||||
| 68,0 | 41,0 | 8,0 | 34,0 | ||||||
| 38,0 | 19,0 | 7,4 | 19,0 | ||||||
| 93,2 | 49,5 | 14,0 | 46,6 | ||||||
| 117,0 | 55,2 | 25,0 | 58,5 | ||||||
| 42,0 | 21,0 | 10,2 | 24,2 | ||||||
| 62,0 | 35,0 | 11,0 | 35,7 | ||||||
| 89,0 | 52,3 | 11,5 | 51,2 | ||||||
| 132,0 | 89,6 | 11,0 | 75,9 | ||||||
| 40,8 | 19,2 | 10,1 | 21,2 | ||||||
| 59,2 | 31,9 | 11,2 | 30,8 | ||||||
| 65,4 | 38,9 | 9,3 | 34,0 | ||||||
| 60,2 | 36,3 | 10,9 | 31,9 | ||||||
| 82,2 | 49,7 | 13,8 | 43,6 | ||||||
| 98,4 | 52,3 | 15,3 | 52,2 | ||||||
| 76,7 | 44,7 | 8,0 | 43,1 | ||||||
| 38,7 | 20,0 | 10,2 | 25,0 | ||||||
| 56,4 | 32,7 | 10,1 | 35,2 | ||||||
| 76,7 | 44,7 | 8,0 | 40,8 | ||||||
| 38,7 | 20,0 | 10,2 | 18,2 | ||||||
| 41,5 | 20,0 | 10,2 | 20,1 | ||||||
| 48,8 | 28,5 | 8,0 | 22,7 | ||||||
| 57,4 | 33,5 | 10,1 | 27,6 | ||||||
| 76,7 | 44,7 | 8,0 | 36,0 | ||||||
| 37,0 | 17,5 | 8,3 | 17,8 | ||||||
| 54,0 | 30,5 | 8,3 | 25,9 | ||||||
| 68,0 | 42,5 | 8,3 | 32,6 | ||||||
| 40,5 | 16,0 | 11,0 | 19,8 | ||||||
| 61,0 | 31,0 | 11,0 | 29,9 | ||||||
| 80,0 | 45,6 | 11,0 | 39,2 | ||||||
| 52,0 | 21,2 | 11,2 | 22,4 | ||||||
| 78,1 | 40,0 | 11,6 | 35,2 | ||||||
| 91,6 | 53,8 | 16,0 | 41,2 | ||||||
| 39,9 | 19,3 | 8,4 | 17,8 | ||||||
| 56,2 | 31,4 | 11,1 | 25,0 | ||||||
| 79,1 | 42,4 | 15,5 | 35,2 | ||||||
| 91,6 | 55,2 | 9,4 | 40,8 | ||||||
| Принятые в таблице обозначения: y-цена квартиры, тыс.долл.; x1 - число комнат в квартире; x2 – район города (1 – Приморский, Шувалово – Озерки, 2 – Гражданка, 3 – Юго-Запад, 4 – Красносельский); x3 - общая площадь квартиры (м2); x4 – жилая площадь квартиры (м2); x5 - площадь кухни (м2); x6 – тип дома (1- кирпичный, 0 – другой); x7 – наличие балкона (1 – есть, 0 – нет); x8 – число месяцев до окончания срока строительства. |
Задание
1. Определите факторы, формировавшие цену квартир в строящихся |Санкт-Петербурге в 1996 г. Сгенерируйте фиктивную переменную z, отражающую местоположение квартиры и позволяющую разделить всю совокупность квартир на две группы: квартиры ч севере города (Приморский район, Шувалово-Озерки, Гражданка) и на юге города (Юго-Запад, Красносельский район).
2. Составьте матрицу парных коэффициентов корреляции:
а) исходных переменных;
б) логарифмов исходных переменных (кроме фиктивных переменных). Вместо переменной х2 используйте фиктивную переменную г
3. Постройте уравнение регрессии, характеризующее зависимость цены от всех факторов, в линейной и степенной форме. Установите какие факторы мультиколлинеарны. В какой модели мультиколлинеарность проявляется сильнее?
4. Постройте модель у = f (x3, x6, x7, x8, z) в линейной и степенной форме. Какие факторы значимо воздействуют на формирование цены квартиры в этой модели?
5. Существует ли разница в ценах квартир, расположенных в северной и южной частях Санкт-Петербурга? Является ли наличие балкона или лоджии преимуществом квартиры на рынке? Как вы объясните этот факт?
Задача 4.
По данным, представленным в табл. 2.2.13, изучается зависимость индекса человеческого развития у от переменных:
X1 - ВВП 1997 г., % к 1990 г.;
X2 - расходы на конечное потребление в текущих ценах, % к ВВП;
хз - расходы домашних хозяйств, % к ВВП;
Xt - валовое накопление, % к ВВП;
Х5 - суточная калорийность питания населения, ккал на душу населения;
Х6- ожидаемая продолжительность жизни при рождении 1997г.
число лет.
Таблица 2.2.13
| Страна | у | Xi | Xi | Хз | Х4 | Xs | Х6 |
| Австрия | 0,904 | 115,0 | 75,5 | 56,1 | 25,2 | 77,0 | |
| Австралия | 0,922 | 123,0 | 78,5 | 61,8 | 21,8 | 78,2 | |
| Белоруссия | 0,763 | 74,0 | 78,4 | 59,1 | 25,7 | 68,0 | |
| Бельгия | 0,923 | 111,0 | 77,7 | 63,3 | 17,8 | 77,2 | |
| Великобритания | 0,918 | 113,0 | 84,4 | 64,1 | 15,9 | 77,2 | |
| Германия | 0,906 | 110,0 | 75,9 | 57,0 | 22,4 | 77,2 | |
| Дания | 0,905 | 119,0 | 76,0 | 50,7 | 20,6 | 75,7 | |
| Индия | 0,545 | 146,0 | 67,5 | 57,1 | 25,2 | 62,6 | |
| Испания | 0,894 | 113,0 | 78,2 | 62,0 | 20,7 | 78,8 | |
| Италия | 0,900 | 108,0 | 78,1 | 61,8 | 17,5 | 78,2 | |
| Швеция | 0,932 | 113,0 | 78,6 | 58,6 | 19,7 | 79,0 | |
| Казахстан | 0,740 | 71,0 | 84,0 | 71,7 | 18,5 | 67,6 | |
| Китай | 0,701 | 210,0 | 59,2 | 48,0 | 42,4 | 69,8 | |
| Латвия | 0,744 | 94,0 | 90,2 | 63,9 | 23,0 | 68,4 | |
| Нидерланды | 0,921 | 118,0 | 72,8 | 59,1 | 20,2 | 77,9 | |
| Норвегия | 0,927 | 130,0 | 67,7 | 47,5 | 25,2 | 78,1 | |
| польша | 0,802 | 127,0 | 82,6 | 65,3 | 22,4 | 72,5 | |
| Россия | 0,747 | 61,0 | 74,4 | 53,2 | 22,7 | 66,6 | |
| США | 0,927 | 117,0 | 83,3 | 67,9 | 18,1 | 76,7 | |
| Украина | 0,721 | 46,0 | 83,7 | 61,7 | 20,1 | 68,8 | |
| Финляндия | 0,913 | 107,0 | 73,8 | 52,9 | 17,3 | 76,8 | |
| Франция | 0,918 | 110,0 | 79,2 | 59,9 | 16,8 | 78,1 | |
| Чехия | 0,833 | 99,2 | 71,5 | 51,5 | 29,9 | 73,9 | |
| Швейцария | 0,914 | 101,0 | 75,3 | 61,2 | 20,3 | 78,6 | |
| Швеция | 0,923 | 105,0 | 79,0 | 53,1 | 14,1 | 78,5 |
Задание
1. Постройте матрицу парных коэффициентов корреляции. Рассчитайте коэффициенты множественной детерминации, используя в качестве зависимой переменной каждый фактор. Установите, какие факторы мультиколлинеарны.
2. Постройте уравнение множественной регрессии в линейной форме с полным набором факторов.
3. Оцените статистическую значимость уравнения регрессии и его параметров с помощью критериев Фишера и Стьюдента.
4. Отберите информативные факторы по пп.1 и 3. Постройте уравнение регрессии со статистически значимыми факторами.
Задание 5.
Имеются данные по странам за 1997 г. (табл. 2.2.14).
Таблица 2.2.14
| Страна | Индекс человеческого развития, у | Ожидаемая продолжительность жизни при рождении в 1997 г., лет, Xi | Суточная калорийность питания населения, ккал на душу, X2 |
| Австрия | 0,904 | 77,0 | |
| Австралия | 0,922 | 78,2 | |
| Аргентина | 0,827 | 72,9 | |
| Белоруссия | 0,763 | 68,0 | |
| Бельгия | 0,923 | 77,2 | |
| Бразилия | 0,739 | 66,8 | |
| Великобритания | 0,918 | 77,2 | |
| Венгрия | 0,795 | 70,9 | |
| Германия | 0,906 | 77,2 | |
| Греция | 0,867 | 78,1 | |
| Дания | 0,905 | 75,7 | |
| Египет | 0,616 | 66,3 | |
| Израиль | 0,883 | 77,8 | |
| Индия | 0,545 | 62,6 | |
| Испания | 0,894 | 78,0 | |
| Италия | 0,900 | 78,2 | |
| Канада | 0,932 | 79,0 | |
| Казахстан | 0,740 | 67,7 | |
| Китай | 0,701 | 69,8 | |
| Латвия | 0,744 | 68,4 | |
| Нидерланды | 0,921 | 77,9 | |
| Норвегия | 0,927 | 78,1 | |
| Польша | 0,802 | 72,5 | |
| Республика Корея | 0,852 | 72,4 | |
| Россия | 0,747 | 66,6 | |
| Румыния | 0,752 | 69,9 | |
| США | 0,927 | 76,6 | |
| Турция | 0,728 | 69,0 | |
| Украина | 0,721 | 68,8 | |
| Финляндия | 0,913 | 76,8 | 2916. |
| Франция | 0,918 | 78,1 | |
| Чехия | 0,833 | 73,9 | |
| Швейцария | . 0,914 | 78,6 | |
| Швеция | 0,923 | 78,5 | 3160, |
| ЮАР | 0,695 | 64,1 | |
| Япония | 0,924 | 80,0 |
Задание
1. Постройте матрицу парных коэффициентов корреляции.
2. Постройте парные уравнения регрессии.
3. Оцените статистическую значимость уравнений и их параметров с помощью критериев Фишера и Стьюдента.
4. Постройте уравнение множественной регрессии.
5. Постройте графики остатков. Сделайте выводы.
6. Проведите тестирование ошибок уравнения множественной регрессии на гетероскедастичность, применив тест Гельфельда-Квандта.
7. Оцените статистическую значимость уравнения множественной регрессии. Определите, какое уравнение лучше использовать для прогноза:
¨ парную регрессию у на х1
¨ парную регрессию у на х 2;
¨ множественную регрессию.
Задача 6.
Изучается зависимость средней ожидаемой продолжительности y от нескольких факторов по данным за 1995 г., представленным табл. 2.21.
Таблица 2.2.15