Характеристика моделей с распределенным лагом и моделей авторегрессии
Многие экономические процессы имеют временной характер изменения. Поэтому в эконометрике рассматриваются так называемые динамические модели.
Эконометрическая модель является динамической, если в данный момент времени t она учитывает значения входящих в нее переменных, относящихся как к текущему, так и к предыдущим моментам времени.
Выделяют два основных типа динамических эконометрических моделей.
К моделям 1-го типа относятся модели авторегрессии и модели с распределенным лагом, в которых значения переменной за прошлые периоды времени (лаговые переменные) непосредственно включены в модель. Модели 2-го типаучитывают динамическую информацию в неявном виде. В этих моделях присутствуют переменные, характеризующие ожидаемый или желаемый уровень результата, или одного из факторов в момент времени t. Этот уровень считается неизвестным, и определяются экономическими единицами с учетом информации, которой они располагают в момент (t-1).
В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адаптивных ожиданий и рациональных ожиданий. Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.
При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение результативного признака в момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени (t-1),(t-2),..(t-k). Например, выручка от реализации и прибыль компании текущего периода зависят от расходов на рекламу или проведенных маркетинговых исследований, сделанных компаний в предшествующие моменты времени.
Величину k, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самых факторных переменных, сдвинутые на один или более моментов времени, - лаговыми переменными.
Основная проблема экономической политики как на макро-, так и на микроуровне это решение обратного типа задач, т.е. задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей. Например, как повлияют инвестиции в промышленность на валовую добавленную стоимость этой отрасли экономики будущих периодов.
Модели экономических процессов, содержащие не только текущие, но и лаговые значения факторных переменных называются моделями с распределенным лагом.
Например, модель

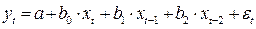
является моделью с распределенным лагом.
Если на величину зависимой переменной текущего периода (уt) оказывают влияние ее значения в прошлые моменты времени (yt-1, yt-2,…), то эти процессы обычно описываются с помощью моделей авторегрессии. Например,

Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику:
оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК и требует специальных статистических методов;
приходится решать проблему выбора оптимальной величины лага и определения его структуры;
между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.
Рассмотрим модель с распределенным лагом в ее общем виде:

 (7.1)
(7.1)
Коэффициент  характеризует среднее абсолютное изменение уt при изменении хt на единицу в момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
характеризует среднее абсолютное изменение уt при изменении хt на единицу в момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
В момент (t+1) совокупное воздействие факторной переменной х  на результат y
на результат y  составит (
составит (  ) условных единиц, в момент (t+2) это воздействие можно охарактеризовать суммой (
) условных единиц, в момент (t+2) это воздействие можно охарактеризовать суммой ( 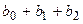 ) и т. д.. Полученные таким образом новые коэффициенты называют промежуточными мультипликаторами.
) и т. д.. Полученные таким образом новые коэффициенты называют промежуточными мультипликаторами.
Введем обозначение

Величину b называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t+ 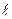 результата у под влиянием изменения на единицу фактора х.
результата у под влиянием изменения на единицу фактора х.
Положим
 .
.
Полученные величины называются относительными коэффициентами модели с распределенным лагом.
Очевидно, что если 0<  <1 и
<1 и 
В этом случае относительные коэффициенты 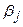 являются весами для соответствующих коэффициентов
являются весами для соответствующих коэффициентов  j. Каждый из них изменяет долю общего изменения результативного признака в момент времени (t+j). На основе величин
j. Каждый из них изменяет долю общего изменения результативного признака в момент времени (t+j). На основе величин 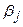 можно определить две важные характеристики модели множественной регрессии: величину среднего и медианного лага.
можно определить две важные характеристики модели множественной регрессии: величину среднего и медианного лага.
Средний лаг определяется по формуле  и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, высокое его значение о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, высокое его значение о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени.
Медианный лаг - это величина лага, для которого  .
.
Это тот период времени, в течение которого будет реализована половина общего воздействия фактора на результат.
Рассмотрим теперь модель авторегрессии:
 (7.2)
(7.2)
Параметров b 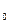 имеет тот же смысл, что и в модели с распределенным лагом (1).Общее абсолютное изменение результата в момент (t+1) составит
имеет тот же смысл, что и в модели с распределенным лагом (1).Общее абсолютное изменение результата в момент (t+1) составит  , в момент времени (t+2) абсолютное изменение результата составит
, в момент времени (t+2) абсолютное изменение результата составит  единиц и т.д.
единиц и т.д.
Долгосрочный мультипликатор в модели авторегрессии рассчитывается как сумма как сумма краткосрочного и промежуточных мультипликаторов:  (7.3)
(7.3)
Обычно во всех моделях авторегрессии вводится условие стабильности, состоящее в том, что коэффициент регрессии при переменной  по абсолютной величине меньше единицы (
по абсолютной величине меньше единицы (  <1).
<1).
Следовательно, можно написать:
 . (7.4)
. (7.4)