Распределение Гаусса
U
q(u) = 1/Ö2pò eu2/2du,
который называют нормированной функцией Лапласа. В таблице, содержащей значения функции Лапласа, приведены доверительные вероятности только для положительных значений u, поскольку нормированное нормальное распределение симметрично. Для нахождения доверительной вероятности того, что случайная величина (случайная погрешность) попадет в заданный интервал, табличные значения вероятности следует увеличить вдвое. Так, можно показать, что если случайная погрешность при многократном измерении не превышает соответственно ±s, ±2s и ±3s, то доверительные вероятности равны 0,6826; 0,9544 и 0,9973. Т.к. u= (х - m)/s, то рассматриваемые интервалы составляют u=±1, u=±2, u =±3.
Благодаря функции Лапласа можно рассчитать доли брака и выхода годной продукции в зависимости от степени рассеяния контрольного показателя продукции и относительного положения значения математического ожидания и границ поля допускаемых отклонений.
Последовательность вычислений при этом такая:
1. Рассчитывают математическое ожидание генеральной совокупности или среднее арифметическое выборки m.
2. Рассчитывают стандартное отклонение результата измерения.
3. Находят границы допусков (хmax, xmin) и вычисляют расстояния между математическим ожиданием и границами допусков (хmax - m) и (xmin - m.).
4.Выражают в долях стандартного отклонения положение границ поля допуска, т.е. расстояние между математическим ожиданием и границами поля допусков (u). u* = (xmin - m.)/s, u** =(хmax - m)/s
5. По таблицам функции Лапласа находят вероятности Р* и Р**, соответствующие значениям u* и u**. Величина Р* + Р** соответствует доле годного продукта, находящегося в заданных пределах.
6. Брак составит: a = 1 - Р* - Р**.
t - распределение.
t- распределение характеризует степень приближения параметров выборки к генеральной совокупности (нормальному распределению) в зависимости от числа степеней свободы f = n - 1, где n - число измерений, равное числу параллельных проб.
Чем меньше число степеней свободы, тем менее надежной характеристикой генеральной дисперсии s2 является выборочная дисперсия S2. При нормальном распределении появление больших погрешностей менее вероятно, чем малых, поэтому при уменьшении числа параллельных проб вероятность появления больших погрешностей уменьшается. Не учет этого приводит к необъективному, заниженному значению погрешности. Эта ненадежность, связанная с числом определений (параллельных проб), учитывается t-распределением Стьюдента, в котором предусматривается большая вероятность появления больших погрешностей, а малых меньше, чем в нормальном распределении.
Как и нормальное распределение, t-распределение симметрично и имеет максимум при том же значении абсциссы, при котором он был при нормальном распределении. Однако такие характеристики кривой t-распределения, как высота и ширина, зависят от числа степеней свободы, т.е. от числа измерений.
При f ® ¥ t-распределение переходит в нормальное распределение. Практически эта разница становится малозаметной уже при f ³ 20.
| Уравнение | Особенности | Примеры |
Р(х) = 1/(sÖ2p)*ехр((xi – а)2/2s2)

| Вероятность появления наблюдения максимальна на m, также она зависит от множества независимых СВ. Дисперсия = 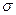 2.Среднее, мода и медиана равны. Асимметрия и эксцесс = 0. Обратная функция стандартного распределения для 0<Z<1 называется пробитом. ±2 2.Среднее, мода и медиана равны. Асимметрия и эксцесс = 0. Обратная функция стандартного распределения для 0<Z<1 называется пробитом. ±2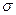 = 95.45%±3 = 95.45%±3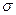 = 99.73%. Стандартный вид при m = 0 и = 99.73%. Стандартный вид при m = 0 и 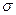 = 1. = 1.
| Разброс значений налюдений при измерении концентрации химических соединений в различных объектах |
