Модели биполярных транзисторов
При анализе транзисторных схем транзистор заменяют эквивалентной схемой, обладающей теми же свойствами, что и транзистор. Существует большое количество различных схем замещения транзисторов. Применение той или иной схемы зависит от режима работы транзистора, частоты сигналов, мощности транзистора и т. д. Схемы замещения транзистора можно разделить на две группы: схемы, базирующиеся на представлении транзистора как линейного четырехполюсника и схемы, составленные на основе анализа уравнений, описывающих физические процессы в транзисторе.
Для анализа транзисторных схем, работающих при малом сигнале и низких частотах удобно использовать эквивалентные схемы, основанные на представлении транзистора как активного линейного четырехполюсника. Достоинством таких схем является их простота и возможность определения параметров элементов схем непосредственно по характеристикам транзистора. На параметры элементов замещения схемы влияют схема включения транзистора, режим работы и температура окружающей среды.
Рассмотрим эквивалентные схемы транзистора на низких частотах, включенного по схеме с общим эмиттером.
В общем случае транзистор можно представить в виде активного нелинейного четырехполюсника (рис.4.7).
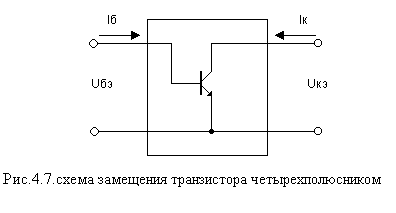
Связь между токами и напряжениями четырехполюсника выражается в виде нелинейных уравнений. В зависимости от того, какие две величины четырехполюсника принять за зависимые, а какие за независимые, можно получить шесть различных нелинейных систем уравнений. Если в качестве зависимых величин выбрать токи базы и коллектора, а независимыми величинами – напряжения база-эмиттер и коллектор-эмиттер, то уравнения можно записать в следующем виде:
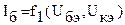 (4.3)
(4.3)
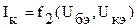 . (4.4)
. (4.4)
Если транзистор работает при малых отклонениях сигнала в рабочей точке, то полные мгновенные значения токов и напряжений можно представить в виде суммы двух составляющих: постоянной – значения тока или напряжения в рабочей точке и переменной – изменения (приращения) тока или напряжения.
Iб = Iб0 + dIб,
Iк = Iк0 + dIк,
Uбэ = Uбэ0 + dUбэ,
Urэ = Urэ0 + dUrэ,
где Iб0, Iк0, Uбэ0, Urэ0, - постоянные значения токов и напряжений в рабочей точке, dIб,
dIк, dUбэ, dUrэ – переменные, малые отклонения токов и напряжений в окрестности рабочей точки. Постоянные значения токов базы и коллектора имеют вид:
Iб0 = f (Uбэ0, Urэ0),
Iк0 = f(Uбэ0, Urэ0).
Разлагая уравнения (4.3) и (4.4) в ряд Тейлора в окрестности рабочей точки Iб0, Iк0 и пренебрегая нелинейными членами ряда в виду их малости, получим:
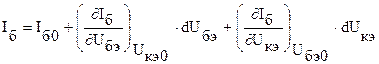 ,
,
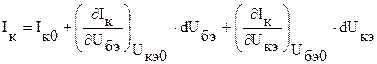 .
.
Найдем переменные составляющие токов в окрестности рабочей точки
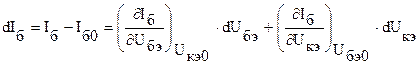 ,
,
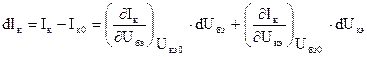 .
.
Здесь частные производные, определяемые в рабочей точке, представляют собой y - параметры транзистора. Легко видеть, что y-параметры транзистора имеют вполне определенный физический смысл:
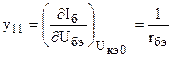 - проводимость база-эмиттер,
- проводимость база-эмиттер,
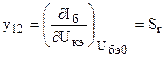 - обратная крутизна,
- обратная крутизна,
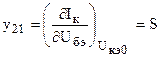 - крутизна,
- крутизна,
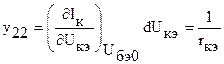 - проводимость коллектор-эмиттер.
- проводимость коллектор-эмиттер.
Параметры транзистора – дифференциальные и зависят от выбранной рабочей точки, т.е. от режима работы транзистора по постоянному току. Запишем уравнения транзистора в окончательном виде
 ,
,
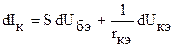 .
.
Полученные уравнения обладают следующими особенностями:
1) система уравнений линейная с постоянными коэффициентами;
2) уравнения составлены не для полных величин токов и напряжений, а для изменений, приращений, т.е. для переменных составляющих;
3) уравнения приближенно описывают работу транзистора, т.к. при выводе не учитывались нелинейные члены ряда в разложении функций. Нелинейными членами ряда можно пренебречь только при малых изменениях токов и напряжений в окрестности рабочей точки;
4) коэффициенты уравнений легко могут быть определены по характеристикам транзистора.
Проведенный вывод уравнений соответствует замене нелинейных характеристик транзистора касательными в рабочей точке и переносе начала координат в рабочую точку. При этом переменными являются не полные значения токов и напряжений, а их приращения, изменения (переменные составляющие). Свойства транзистора характеризуются дифференциальными параметрами: крутизной S, сопротивлением база-эмиттер rбэ, сопротивлением коллектор-эмиттер rкэ. Обратная крутизна Sr определяет обратную связь транзистора, ее величина мала и часто не учитывается.
На рис.4.8. показана эквивалентная схема транзистора, соответствующая y - параметрам. Обратная связь в транзисторе, определяемая обратной крутизной Sr в этой схеме не учитывается.

Если за независимые величин выбрать напряжение Uбэ и ток коллектора Iк , а за независимые величины – ток базы I, и напряжение коллектор-эмиттер, то уравнения можно записать в следующем виде:
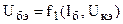
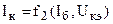 .
.
Выполняя аналогичные математические выкладки, получим уравнения транзистора в h – параметрах
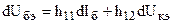 ,
,
 ,
,
где
 при Uкэ= const, входное сопротивление;
при Uкэ= const, входное сопротивление;
 при Uбэ= const, коэффициент обратной передачи по напряжению транзистора;
при Uбэ= const, коэффициент обратной передачи по напряжению транзистора;
 при Uкэ= const, коэффициент передачи по току транзистора;
при Uкэ= const, коэффициент передачи по току транзистора;
 при Uкэ= const, выходная проводимость.
при Uкэ= const, выходная проводимость.
Уравнения транзистора в y и h – параметрах эквивалентны. Одни параметры могут быть выражены через другие:
 ,
,  ,
,
 ,
,  .
.
Для анализа схем можно использовать любую из рассмотренных систем уравнений.