Применение рядов для приближенных вычислений

Применение рядов позволяет с заданной точностью вычислять значение функций, определенных интегралов, находить частные решения дифференциальных уравнений и т. п. Основной трудностью при этом является оценка точности вычислений. Данную трудность преодолевают с помощью оценки остаточного члена ряда.

Если остаточный член ряда представлен с помощью функции , то необходимо найти - количество членов ряда, учитываемых при расчете, при котором остаточный член не превзойдет требуемой точности вычисления e, т. е. .

Если остаточный член представлен в виде знакочередующегося ряда , то оценка погрешности вычисления является наиболее простой. В этом случае применяют терему Лейбница, согласно которой сумма ряда (остатка ряда) по абсолютной величине не превосходит первого отброшенного члена ряда.

Если же остаточный член представляет знакопостоянный ряд , то для его оценки необходимо составить так называемый можарирующий ряд. Данный ряд обычно является бесконечно убывающей геометрической прогрессией, сумма которой легко находится.

Пример 9.6. Вычислить значение числа е с точностью .

Используем разложение показательной функции в ряд Маклорена

, где , .

Область сходимости .

При имеем .

Число n членов ряда, которые необходимо учесть, чтобы остаток ряда не превосходил заданной точности расчета , найдем из неравенства

Будем считать известным, что . Тогда условие для нахождения числа n примет вид . В ниже следующей таблице приведены оценки остаточного члена ряда при различных значениях

Число n, учитываемых членов ряда
Оценка остаточного члена ряда						<

Как видно из таблицы, при остаточный член ряда . Следовательно, для того, чтобы вычислить число е с погрешности не превосходящей , нужно учесть шесть членов в разложении. При вычислениях учитываем на один десятичный знак больше, чем . В окончательном результате этот последний десятичный знак отбрасываем.

Получаем

Окончательно принимаем .

Для сравнения более точное значение .

Пример 9.7. Вычислить значение функции при с точностью .

Используем разложение в ряд Маклорена

Область сходимости этого ряда .

При имеем

Данный ряд и любой его остаток является знакочередующимся. Любой остаток ряда не превзойдет по абсолютной величине первого члена ряда. Это значит, что для вычисления значения с точностью можно отбросить все члены, начиная с , который меньше 0,0001.

Вычисляем

Округляем с точностью до , получаем .

Для сравнения, более точное значение .

Пример 9.8. Вычислить значение корня с точностью .

Используем разложение в ряд Маклорена функции

Интервал сходимости этого ряда .

Если представить в виде , то вычисление с помощью этого ряда приведет к неверному результату, так как значение находится вне области сходимости ряда.

Если представить искомый корень в виде , так что , то при разложении в ряд получится знакопостоянный (знакоотрицательный) ряд

В этом случае оценка погрешности вычислений приведет к некоторым затруднениям (составление так называемого можарирующего ряда). Лучше избежать этого и представить в виде . Тогда и получится знакочередующийся ряд. Оценка погрешности в этом случае достаточно простая, с помощью теоремы Лейбница.

Вычисляем

Седьмой член в разложении, равный примерно , меньше . Его и все последующие члены можно отбросить; при этом погрешность вычисления не превзойдет заданной точности. Округляем результат до 0,0001, получаем .

Для сравнения более точное значение .

Пример 9.9. Вычислить , где N некоторое положительное число.

Для этого используют разложение функции в ряд Маклорена

Интервалом сходимости данного ряда является .

Для того, чтобы вычислить значение при производят следующее преобразование. Находят разложение в ряд Маклорена для функции .

Учитывая, что , найдем разность двух рядов

Получаем

Областью сходимости данного ряда также является интервал .

Чтобы вычислить , приравняем и найдем отсюда х, Þ . При любом значении данное значение х всегда меньше единице и, следовательно, для вычисления значения можно применять полученное разложение. Рассмотрим конкретный пример.

Пример 9.10. Вычислить с заданной точностью .

При находим .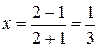

Записываем

Чтобы вычислить с заданной точностью, необходимо оценить остаток ряда, который является знакоположительным рядом.

Составим можарирующий ряд, члены которого больше соответствующих членов этого остатка ряда.

Вынесем за скобки первый член остатка ряда

Очевидно , , поэтому заменим эти дроби единицей (усилим неравенство), имеем

Найдем сумму бесконечной убывающей геометрической прогрессии, получим

Найдем n, при котором .

Имеем Þ.

При .

Таким образом, для достижения требуемой точности нужно принять .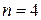

Вычисляем

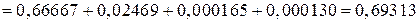
Более точное значение, полученное с помощью калькулятора, .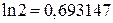

Пример 9.11. Вычислить интеграл с точностью .

Данный интеграл относится к числу неберущихся и называется интегральным синусом.

Разложим в ряд и проинтегрируем, получим

Здесь для оценки погрешности использовали теорему Лейбница.

Пример 9.12. Найти частное решение дифференциального уравнения при .

Ищем решение в виде ряда

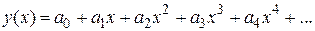При отсюда имеем .

Продифференцируем ряд почленно

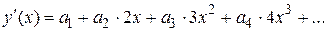
и подставим и в дифференциальное уравнение

Приравняем коэффициенты при одинаковых степенях х в левой и правой частях этого равенства, получим:

Далее, очевидно, можно аналогично получить .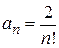

Записываем частное решение дифференциального уравнения

Решим данное уравнение аналитическим методом. Запишем уравнение в виде . Найдем общее решение соответствующего однородного уравнения . Характеристическое уравнение этого уравнения имеет один корень . Общее решение однородного уравнения имеет вид . Частное решение исходного неоднородного уравнения ищем в виде 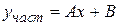. Подставляем его в уравнение, получаем

Приравниваем коэффициенты при одинаковых степенях х, получаем

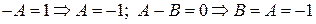. Частное решение 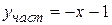. Общее решение исходного уравнения имеет вид . Используем начальные условия для нахождения произвольной постоянной С . Таким образом частное решение имеет тот же вид , что и при использовании разложения решения в степенной ряд Маклорена.