Знакочередующиеся ряды. Теорема Лейбница
Теорема 8.7.Если члены знакочередующегося ряда  монотонно убывают
монотонно убывают  и стремятся к нулю
и стремятся к нулю 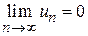 , то ряд сходится; причем сумма ряда по абсолютной величине не превосходит первого члена ряда
, то ряд сходится; причем сумма ряда по абсолютной величине не превосходит первого члена ряда  .
.
Д о к а з а т е л ь с т в о. По определению знакочередующегося ряда

предполагается, что члены ряда положительные  .
.
Рассмотрим две частичные суммы ряда: с четным числом членов ряда  и с нечетным числом членов
и с нечетным числом членов  .
.
В сумме с четным числом членов  сначала сгруппируем члены попарно следующим образом
сначала сгруппируем члены попарно следующим образом
 .
.
Так как члены ряда монотонно убывают ( ), то разность в каждой скобке суммы
), то разность в каждой скобке суммы  больше нуля и эта сумма монотонно возрастает с увеличением числа членов 2n.
больше нуля и эта сумма монотонно возрастает с увеличением числа членов 2n.
Теперь сгруппируем члены этой суммы следующим образом
 .
.
Так как в этой сумме также разность в каждой скобке больше нуля, то сумма монотонно убывает с увеличением числа членов 2n и не превосходит первого члена ряда  .
.
Следовательно, последовательность частичных сумм ряда с четным числом членов монотонно возрастает и ограничена. Поэтому по теореме Вейерштрасса она имеет некоторый предел  .
.
Найдем также предел частичных сумм ряда с нечетным числом членов.
 .
.
При нечетном числе членов ряда сумма  также не превосходит первого члена ряда
также не превосходит первого члена ряда  .
.
 .
.
Таким образом, предел частичных сумм знакочередующегося ряда существует, т. е. ряд всегда сходится, если его члены монотонно убывают и стремятся к нулю.
Частичные суммы знакочередующегося ряда меньше первого члена ряда
 . Члены ряда стремятся к нулю
. Члены ряда стремятся к нулю 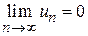 , поэтому сумма ряда не может превосходить первого члена ряда
, поэтому сумма ряда не может превосходить первого члена ряда  .
.
Пример 8.17. Исследовать сходимость ряда  .
.
Члены ряда монотонно убывают  и стремятся к нулю
и стремятся к нулю  . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Пример 8.18. Исследовать сходимость ряда  .
.
Предел членов ряда при неограниченном возрастании их номеров отличен от нуля  . По следствию необходимого признака сходимости числовых рядов рассматриваемый ряд расходится.
. По следствию необходимого признака сходимости числовых рядов рассматриваемый ряд расходится.