Интегральный признак Коши

Теорема 8.6. Если члены знакоположительного ряда , являющиеся значениями функции целочисленного аргумента , монотонно убывают и стремятся к нулю 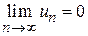, то: 1) если сходится, то и ряд сходится; 2) если расходится, то и ряд расходится.

Д о к о з а т е л ь с т в о. В прямоугольной декартовой системе координат непрерывная кривая проходит через точки и ограничивает сверху криволинейную трапецию ABCD (рис. 86). Площадь этой криволинейной трапеции равняется .

Построим две ступенчатые фигуры с угловыми точками . Эти ступенчатые фигуры состоят из прямоугольников, основания которых равняются единице, а высоты значениям .

Рис. 86

Найдем площади этих фигур.

где - n-я частичная сумма ряда.

Площади этих ступенчатых фигур ограничивают площадь криволинейной трапеции ABCD снизу и сверху

Û .

Рассмотрим левую часть этого неравенства

Û.

При неограниченном возрастании числа n членов ряда частичные суммы ряда монотонно возрастают, так как ряд знакоположительный. При этом интеграл также возрастает и ограничен величиной интеграла . Поэтому , т. е. последовательность частичных сумм ограничена. По теореме Вейерштрасса существует предел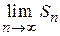. Следовательно, ряд сходится.

Рассмотрим правую часть неравенства

Û.

По условию теоремы .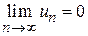

Если неограниченно возрастает, то и предел частичных сумм 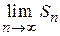неограниченно возрастает и, следовательно, ряд расходится.

Таким образом, интегральный признак Коши в принципе позволяет для любого ряда решить вопрос о его сходимости. Трудность в его применении заключается в нахождении несобственных интегралов. Возможности в их нахождении ограниченные.

Пример 8.13. Исследовать гармонического сходимость ряда .