Метод Эйлера численного интегрирования дифференциальных уравнений

Метод Эйлера является самым простым из множества методов численного интегрирования дифференциальных уравнений.

Пусть для дифференциального уравнения на отрезке требуется решить задачу Коши, т. е. необходимо найти решение дифференциального уравнения , удовлетворяющее начальным условиям , где - некоторое заданное значение, .

Разобьем отрезок на n элементарных отрезков длиной с помощью точек . На каждом элементарном отрезке заменим интегральную кривую касательной к этой кривой (рис. 85) и найдем приближенные значения решения дифференциального уравнения в этих точках .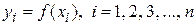

Рис. 85

На первом элементарном отрезке дано значение искомой функции в граничной точке . Найдем приближенное значение функции в правой граничной точке рассматриваемого отрезка.

Получаем

Данное значение является исходным для нахождения значения искомой функции на отрезке , где , .

Получаем

Аналогично вычисляются приближенные значения решения на следующих элементарных отрезках по формулам

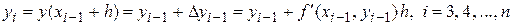Вычисления продолжаются до тех пор, пока значение х достигнет конечной точки отрезка .

Общая схема расчета состоит в том, что сначала проводят расчет при некотором произвольно выбранном значении n, получают значение искомой функции (частного решения) в конечной точке отрезка интегрирования 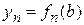. Затем увеличивают число элементарных отрезков (обычно в два раза, 2n). Снова проводят расчет, находят . И сравнивают полученные результаты

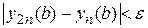где e - заданная точность расчета.

Если два последовательных приближения отличаются друг от друга менее, чем на заданное значение e, то последнее значение функции (решения) принимается за окончательное. Иначе, число элементарных отрезков увеличивается и расчет продолжается.

Пример 7.28. Дифференциальное уравнение при проинтегрировать на отрезке .

Пусть , . Результаты расчета приведены в таблице.

i
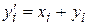
				0,1	1,1
	0,1	1,1	1,2	0,12	1,22
	0,2	1,22	1,42	0,142	1,362
	0,3	1,362	1,662	0,1662	1,5282
	0,4	1,5282	1,9282	0,19282	1,72102
	0,5	1,72102

Следовательно .