Порядок выполнения типового примера.

 

Имеются следующие выборочные данные:

   
№ п/п X1 X2 Y
-69
-67
-62
-77
-78
-63
-72
-79
-74
-68
-67
-72
-73
-66
-71
-66
-76
-73
-67
-69
-59
-76
-78
-82

 
№ п/п X1 X2 Y
-69
-67
-62
-77
-78
-63
-72
-79
-74
-68
-67
-72
-73
-66
-71
-66
-76
-73
-67
-69
-59
-76
-78
-82

 

 

где X1 и X2 - объясняющие или факторные переменные; Y- объясняемая переменная; n = 48 - число выполненных измерений, или объем выборки.

Исследуем зависимость объясняемой переменной Y от факторных переменных Х1 и Х2, используя множественный регрессионный анализ. Для этого необходимо выполнить расчеты:

1. Вычисление осредненных характеристик выборки (допускается выполнение на компьютере, остальные разделы – с помощью калькулятора).

2. Вычисление коэффициентов парной корреляции.

3. Вычисление стандартизованных коэффициентов множественной линейной регрессии и ранжирование с их помощью факторных переменных.

4. Обоснование формы и оценка параметров линейной множественной регрессии.

5. Построение множественной линейной регрессии в естественной форме.

6. Вычисление стандартной ошибки регрессии.

7. Вычисление частных коэффициентов корреляции и частных коэффициентов эластичности.

8. Вычисление коэффициента множественной регрессии и индекса множественной корреляции.

9. Проверка гипотезы о статистической значимости полученного уравнения множественной регрессии

10. Вычисление доверительных интервалов параметров регрессии при уровне значимости a = 0,1 или 0,05.

Каждый из них должен включать:

а) изложение теоретических предпосылок и обоснование расчетных формул;

б) выполнение расчетов;

в) обсуждение полученных результатов.

 

Исследование должно включать в себя наряду с получением оценок статистических характеристик многомерной пространственной выборки обоснование применяемых методов их вычисления, а также элементы экономического анализа.

Выполнение численных расчетов необходимо сопровождать обсуждением экономического содержания полученных результатов. В конце работы на отдельном листе прилагается список использованной методической и учебной литературы.

В таблице 1. показаны вычисления всех средних величин, которые необходимы для проведения этого анализа и вычисления по данным выборки следующих показателей:

Таблица 1

 

№ п/п
-69 -1932 -20562
-67 -2010 -20770
-62 -1798 -18290
-77 -2310 -24332
-78 -2418 -24258
-63 -1827 -19404
-72 -2160 -22248
-79 -2370 -24174
-74 -2146 -22718
-68 -1972 -19924
-67 -2010 -20301
-72 -2088 -21600
-73 -2190 -22703
-66 -1914 -19932
-71 -2059 -21229
-66 -1914 -20064
-76 -2204 -23484
-73 -2117 -21681
-67 -2010 -21105
-69 -2001 -20493
-59 -1711 -18172
-76 -2280 -23104
-78 -2418 -24804
-82 -2624 -27634
-79 -2370 -24964
-64 -1920 -19328
-77 -2387 -24640
-64 -1856 -18624
-71 -2059 -20590
-74 -2368 -23976
-63 -1827 -19152
-68 -1972 -19856
-63 -1827 -19467
-61 -1830 -18483
-67 -2010 -20569
-76 -2356 -25004
-73 -2336 -24528
-77 -2387 -23870
-64 -1920 -19264
-63 -1701 -17010
-73 -2336 -24674
-60 -1680 -16980
-63 -1890 -19215
-82 -2624 -27224
-70 -2100 -21280
-60 -1680 -17580
-73 -2117 -21827
-66 -1782 -18678
S -3355 -99818 -1029769
Среднее значение 29,69 -69,90 306,21 882,77 4923,60 93953,00 -2079,54 9105,23 -21453,52

 

1. Статистические дисперсии:

;

;

;

Стандартные (среднеквадратические) отклонения:

; ;

.

 

Ковариации:

;

.

 

2. Линейные коэффициенты парной корреляции:

;

;

.

Анализируя значения коэффициентов парной корреляции, приходим к следующему выводу:

 

Связанные переменные Теснота связи Направление связи
и сильная прямая
и умеренная обратная
и умеренная обратная

3. Стандартизованные коэффициенты регрессии:

 

;

.

Сравнивая модули значений и , приходим к выводу, что сила влияния фактора Х1 на объясняемую переменную Y намного больше, чем сила влияния фактора Х2.

 

4. Оценки коэффициенты множественной линейной регрессии:

;

;

.

 

5. Уравнение множественной линейной регрессии в естественной форме:

6. Вычисление стандартной ошибки регрессии выполняется с помощью расчетной таблицы 2:

Tаблица 2

№ п/п
-69 289,63 8,37 70,12
-67 308,72 1,28 1,64
-62 298,08 -3,08 9,48
-77 310,54 5,46 29,76
-78 320,46 -9,46 89,42
-63 298,26 9,74 94,84
-72 309,63 -0,63 0,40
-79 310,91 -4,91 24,10
-74 300,27 6,73 45,32
-68 299,17 -6,17 38,11
-67 308,72 -5,72 32,73
-72 299,90 0,10 0,01
-73 309,81 1,19 1,40
-66 298,81 3,19 10,18
-71 299,72 -0,72 0,52
-66 298,81 5,19 26,95
-76 300,63 8,37 70,02
-73 300,09 -3,09 9,52
-67 308,72 6,28 39,43
-69 299,36 -2,36 5,55
-59 297,53 10,47 109,58
-76 310,36 -6,36 40,48
-78 320,46 -2,46 6,03
-82 330,92 6,08 37,02
-79 310,91 5,09 25,92
-64 308,17 -6,17 38,11
-77 320,27 -0,27 0,08
-64 298,44 -7,44 55,41
-71 299,72 -9,72 94,49
-74 329,46 -5,46 29,77
-63 298,26 5,74 32,93
-68 299,17 -7,17 51,46
-63 298,26 10,74 115,31
-61 307,63 -4,63 21,40
-67 308,72 -1,72 2,96
-76 320,09 8,91 79,36
-73 329,27 6,73 45,24
-77 320,27 -10,27 105,56
-64 308,17 -7,17 51,46
-63 278,80 -8,80 77,48
-73 329,27 8,73 76,14
-60 287,98 -4,98 24,85
-63 307,99 -2,99 8,95
-82 330,92 1,08 1,18
-70 309,27 -5,27 27,75
-60 287,98 5,02 25,15
-73 300,09 -1,09 1,18
-66 279,35 3,65 13,33
-3355 14698,00 0,00 1798,07
/n 29,69 -69,90 306,21 306,21 0,00 37,46

 

.

 

7. Частные коэффициенты линейной корреляции:

Сравнение с парными коэффициентами корреляции показывает, что существует слабая взаимосвязь между факторными переменными. Но она сильно проявилась на связи Y и X2, уменьшив характеристику связи с -0,598 до -0,144. На связь Y и X1 она повлияла незначительно ( 0,893 и 0,832 соответственно).

Средние частные коэффициенты эластичности:

При увеличении фактора X1 на 1% от его среднего уровня объясняемая переменная Y возрастает на 0,944 % от среднего уровня, а при увеличении фактора X2 на 1% от его среднего уровня объясняемая переменная Y возрастает на 0,041 % от своего среднего уровня.

8. Характеристика совокупного влияния всех факторов на объясняемую переменную ‑ коэффициент множественной корреляции можно рассчитать несколькими способами:

1) для уравнения регрессии в стандартизованной форме:

2) используя матрицы парных коэффициентов корреляции R’ и R:

,

где - определитель матрицы коэффициентов парной корреляции;

- определитель матрицы межфакторной корреляции, или межфакторного взаимодействия.

Таким образом:

 

3) как корень квадратный из коэффициента множественной детерминации:

На основании значения коэффициента множественной регрессии делается вывод, что зависимость объясняемой переменной от факторов и характеризуется как тесная, в которой 80,2% вариации определяются вариацией данных факторов. Прочие факторы, не включенные в модель, составляют соответственно только 19,8 % от общей вариации .

 

9. Оценивание качества уравнения регрессии с помощью F-критерия Фишера состоит в проверке гипотезы H0 о статистической значимости уравнения регрессии или показателя тесноты связи. Для этого сравнивают фактическое значение критерия с критическим, табличным значением .

где - число объясняющих переменных, или факторов, включенных в модель.

Табличное значение значением находится с помощью таблиц критических точек критерия Фишера:

,

где - уровень значимости; и - число степеней свободы большей (числителя) и меньшей (знаменателя) дисперсий соответственно.

Так как в нашем случае , то гипотеза H0 о случайной природе статистической связи отклоняется. Имеющиеся статистические данные свидетельствуют о том, что в 95 % случаев связь обусловлена влиянием факторов регрессии, а остальные не включенные в нее факторы являются статистически не значимыми. С вероятностью 0,95 делаем заключение о статистической значимости уравнения регрессии в целом и показателя тесноты связи , которые сформировались под неслучайным воздействием факторов Х1 и Х2.

 

10. Найдем доверительные интервалы для коэффициентов регресси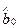и , и .

 

.

 

Табличная величина критерия Стьюдента:

 

.

Дисперсия стандартной ошибки оценки коэффициентов :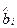

 

1) .

Предельная ошибка выборки оценки коэффициента :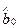

Таким образом, интервальная оценка коэффициента :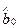

.

 

2) ,

.

Таким образом: ,

.

 

3)

Таким образом:

.