Содержание самостоятельной работы студентов 3 страница
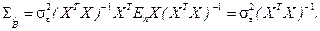(3.5)
Неизвестное значение дисперсии случайного отклонения теоретической регрессии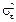 
заменяется соответствующей несмещенной выборочной оценкой 
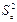(3.2). Следовательно, по выборке мы можем определить только выборочные оценки дисперсий коэффициентов эмпирической регрессии 
, которые являются диагональными элементами матрицы 
:
, (3.6)
где через 
обозначены диагональные элементы обратной матрицы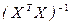 
, j = 0, 1, 2, ..., p.
Стандартные ошибки коэффициентов регрессии вычисляются по формулам:
, (3.7)
где j = 0, 1, ..., p.
4.3. Доверительные интервалы коэффициентов регрессии
Для построения интервальной оценки неизвестных коэффициентов регрессии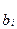 
вводится случайная величина 
- стандартизованный коэффициент регрессии, имеющая распределение Стьюдента с числом степеней свободы 
.
При заданном уровне значимости a доверительный интервал записывается следующим образом:
где 
- табличное значение t-критерия Стьюдента
Из данного неравенства следует:
(3.8)
где 
и 
- стандартная и предельная ошибки выборочных оценок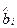 
соответственно.
4.4. Стандартная ошибка и доверительные интервалы уравнения регрессии
Дисперсия многомерной случайной величины 
определяется с помощью ковариационной матрицы 
:
где матрица определена формулой (3.6).
Таким образом, получаем окончательное выражение в матричной форме:
(3.9)
Выборочные оценки дисперсий i-го значения эмпирической регрессии 
, соответствующего i-му набору значений факторов (1, хi1, xi2, …, xip) в i-ой строке матрицы Х исходных данных, располагаются по диагонали матрицы 
:
. (3.10)
Стандартные ошибки оценок значений регрессии вычисляются по формулам:
, (3.11)
где i = 1, 2, ..., n.
Доверительные интервалы для неизвестной функции регрессии 
строятся также с помощью случайной величины 
- стандартизованная переменная, имеющей распределение Стьюдента с числом степеней свободы , i - номер измерения.
Из данного неравенства следует:
, (3.12)
где 
и 
- стандартная и предельная ошибки расчетного значения 
соответственно.
4.5. Статистическая значимость уравнения регрессии
Проверить статистическую значимость уравнения множественной регрессии означает установить, соответствует ли регрессионная модель, принятая для объяснения взаимосвязи между переменными, исходным статистическим данным. Или, другими словами, достаточно ли включенных в уравнение регрессии факторов для описания поведения объясняемой переменной на основе имеющихся выборочных данных.
Проверка значимости уравнения регрессии производится с помощью метода статистического анализа – дисперсионного анализа. Оценивание качества уравнения регрессии с помощью F-критерия Фишера состоит в проверке гипотезы H0 о статистической значимости уравнения регрессии или показателя тесноты связи. В случае, когда нулевая гипотеза отвергается, влияние включенных в регрессию факторов на объясняемую переменную преобладает над ее изменениями в силу других причин.
Для этого сравнивают фактическое значение критерия 
с критическим, табличным значением 
.
,
где 
- число объясняющих переменных, или факторов, включенных в модель.
,
где a - уровень значимости; 
и 
- число степеней свободы большей (числителя) и меньшей (знаменателя) дисперсий соответственно.
Если 
, то гипотеза H0 о случайной природе статистической связи отклоняется. С вероятностью ( 1- a ) делается заключение о статистической значимости уравнения регрессии в целом и показателя тесноты связи 
, которые сформировались под совместным воздействием факторов Х1 и Х2, которое нет оснований считать случайным. В противном случае оснований для отклонения гипотезы H0 нет и данная статистическая связь статистически незначима.
5. Уравнение регрессии в стандартизованной форме
5.1. Стандартизованные переменные
В эконометрике часто используется иной подход к определению параметров множественной регрессии (2.13) с исключенным коэффициентом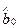 
:
Разделим обе части уравнения на стандартное отклонение объясняемой переменной SY и представим его в виде:
Разделим и умножим каждое слагаемое на стандартное отклонение соответствующей факторной переменной, чтобы перейти к стандартизованным (центрированным и нормированным) переменным:
где новые переменные обозначены как
.
Все стандартизованные переменные имеют нулевую среднюю величину и одинаковую дисперсию, равную единице.
Уравнение регрессии в стандартизованной форме имеет вид:
, (3.1)
где 
- стандартизованные коэффициенты регрессии.
Стандартизованные коэффициенты регрессии 
отличаются от коэффициентов 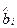обычной, естественной формы тем, что их величина не зависит масштаба измерения объясняемой и объясняющих переменных модели. Кроме того, между ними существует простая взаимосвязь:
, (3.2)
которая дает другой способ вычисления коэффициентов 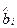по известным значениям , более удобный в случае, например, двухфакторной регрессионной модели.
5.2. Нормальная система уравнений МНК в стандартизованных
переменных
Оказывается, что для вычисления коэффициентов стандартизованной регрессии нужно знать только парные коэффициенты линейной корреляции. Чтобы показать каким образом это делается, исключим из нормальной системы уравнений МНК неизвестную 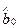с помощью первого уравнения. Умножая первое уравнение на ( 
) и складывая его почленно со вторым уравнением, получим:
Заменяя обозначениями дисперсии и ковариаций выражения в скобках
перепишем второе уравнение в удобном для дальнейшего упрощения виде:
Разделим обе части этого уравнения на стандартное отклонение переменных SY и `SX1, а каждое слагаемое разделим и умножим на стандартное отклонение переменной, соответствующей номеру слагаемого:
Вводя характеристики линейной статистической связи:
,
и стандартизованные коэффициенты регрессии
,
получаем:
.
После аналогичных преобразований всех остальных уравнений ,нормальная система линейных уравнений МНК (2.12) принимает следующий, более простой вид:
(3.3)
5.3. Параметры стандартизованной регрессии
Стандартизованные коэффициенты регрессии в частном случае модели с двумя факторами определяются из следующей системы уравнений:
(3.4)
Решая эту систему уравнений, находим:
, (3.5)
. (3.6)
Подставив найденные значения коэффициентов парной корреляции в уравнения (3.4) и (3.5), получим 
и 
. Затем с помощью формул (3.2) нетрудно вычислить оценки коэффициентов 
и 
, а затем, при необходимости, вычислить оценку 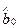по формуле 
6. Возможности экономического анализа на основе многофакторной модели
6.1. Коэффициенты 
стандартизованной регрессии
Стандартизованные коэффициенты регрессии показывают, на сколько стандартных отклонений 
изменится в среднем объясняемая переменная Y, если соответствующая объясняющая переменная Хi изменится на величину 
одного ее стандартного отклонения при сохранении неизменным значений среднего уровня всех остальных факторов.
В силу того, что в стандартизованной регрессии все переменные заданы как центрированные и нормированные случайные величины, коэффициенты сравнимы между собой. Сравнивая их друг с другом, можно ранжировать соответствующие им факторы Хi по силе воздействия на объясняемую переменную Y. В этом состоит основное преимущество стандартизованных коэффициентов регрессии от коэффициентов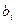 
регрессии в естественной форме, которые несравнимы между собой.
Эта особенность стандартизованных коэффициентов регрессии позволяет использовать при отсеве наименее значимых факторов Хi с близкими к нулю значениями их выборочных оценок 
. Решение об исключении их из модельного уравнения линейной регрессии принимается после проверки статистических гипотез о равенстве нулю его средней величины.
6.2. Средние и частные коэффициенты эластичности
В экономических исследованиях для количественного представления результатов множественного анализа также часто применяют коэффициенты эластичности. Коэффициент эластичности характеризует изменение в процентах объясняемой переменной при изменении факторной переменной на 1% и определяется для зависимости 
как
.
Он имеет четкую экономическую интерпретацию для степенной функции 
. Производная этой функции 
. Оказывается, что коэффициент эластичности при этом равен
и имеет постоянную величину.
Обобщение понятия эластичности на другие формы регрессионной связи приводит к тому, что 
оказывается зависящим от величины факторной переменной. Так для линейной регрессии 
эластичность принимает вид:
.
Поскольку коэффициент эластичности для линейной функции не является постоянной величиной, то вводят средний показатель эластичности:
.
Для характеристики относительной силы влияния каждого фактора в многофакторной регрессии используют частные коэффициенты эластичности:
В частном случае двухфакторной линейной зависимости
для характеристики влияния Х1 и Х2 на Y рассчитывают частные коэффициенты эластичности:
,
.
Экономическая интерпретация этой статистической взаимосвязи является следующей. При увеличении фактора Х1 на 1% от его среднего уровня объясняемая переменная Y изменяется на 
,% своего от среднего уровня, а при увеличении фактора Х2 на 1% от его среднего уровня объясняемая переменная Y изменяется на 
,% от своего среднего уровня.
Направление изменения объясняемой переменной зависит от знака коэффициента при соответствующем факторе.
6.3. Линейные коэффициенты парной, частной и
множественной корреляции
Наиболее обоснованной характеристикой статистической связи является выборочный коэффициент линейной корреляции. При исследовании двухфакторной модели линейные коэффициенты парной корреляции определяются следующим:
,
,
.
Анализируя значения коэффициентов парной корреляции, приходим к выводам относительно силы и направления взаимосвязи между каждой парой переменных. Однако очевидно, что влияние каждой из факторных переменных на объясняемую переменную не может выражаться также просто, как в случае парной регрессии, в силу их взаимосвязи между собой.
Для характеристики влияния каждого фактора множественной регрессии, аналогичной стандартизованным коэффициентам регрессии, на основе парных коэффициентов линейной корреляции рассчитывают частные коэффициенты корреляции. Они также используются при отборе факторов: целесообразность включения того или иного фактора в модель можно обосновывать величиной показателя частной корреляции.
Частные коэффициенты корреляции характеризуют влияние фактора 
на объясняемую переменную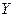 
при устранении влияния других факторов, включенных в уравнение регрессии. В зависимости от их числа вычисляют частные корреляции различного порядка.
В случае двухфакторной модели частные коэффициенты корреляции первого порядка вычисляются непосредственно с помощью парных коэффициентов корреляции по формулам:
Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за сильной связи 
и 
,умеренной связи 
и коэффициенты 
и 
отличаются незначительно, 
и 
- значительно. Выводы о направлении связи на основе этих коэффициентов совпадают.
Когда общее число факторов больше двух и равно р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего, …, (р-1) порядка. Так влияние фактора 
на переменную Y можно оценить при разных способах исключения влияния других факторов: по одному, по два, …, всех (р-2) – ух факторов из числа входящих в регрессию. Хотя частная корреляция различного порядка и может представлять интерес при изучении различных взаимосвязей факторных переменных, на практике ограничиваются вычислением частных корреляций самого высокого порядка. Этими показателями обычно принято дополнять эмпирические модели множественной регрессии
Практическая значимость эмпирического уравнения множественной регрессии оценивается помощью коэффициента множественной корреляции 
или его квадрата 
– коэффициента множественной детерминации.
Коэффициент множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с объясняемой переменной, или оценивает тесноту совместного влияния факторов на результат. Его величина не может быть меньше, чем величина наибольшего коэффициента парной корреляции:
.
При правильном выборе факторов величина коэффициента множественной корреляции должен существенно отличаться от коэффициентов парной корреляции. Целесообразность включения в состав регрессии нового фактора можно обосновать, сравнивая коэффициенты множественной и парной корреляции с его участием.
Коэффициент множественной корреляции можно рассчитать несколькими способами, это полезно делать для контроля правильности вычислений:
1) наиболее просто это сделать для уравнения линейной регрессии в стандартизованной форме:
.
2) используя матрицу парных коэффициентов корреляции:
,
где 
- определитель матрицы коэффициентов парной корреляции;
- определитель матрицы коэффициентов парной корреляции между факторами, или межфакторного взаимодействия.
3) как корень квадратный из коэффициента множественной детерминации:
На основании значения коэффициента множественной регрессии делается вывод о том, что зависимостью переменной у от факторных переменных объясняется R2*100 % вариации, представленной исходными данными. Прочие факторы, не включенные в модель, составляют соответственно ( 1- R2)*100% от общей вариации объясняемой переменной у.
ВАРИАНТЫ КОНТРОЛЬНЫХ ЗАДАНИЙ
Вариант 1
| X | Y | Z | X | Y | Z | X | Y | Z |
| —201 | —237 | —226 | ||||||
| —199 | —209 | —218 | ||||||
| —206 | —243 | —245 | ||||||
| —221 | —239 | —247 | ||||||
| —238 | —221 | —201 | ||||||
| —256 | —238 | —215 | ||||||
| —222 | —238 | —209 | ||||||
| —230 | —223 | —212 | ||||||
| —234 | —207 | —203 | ||||||
| —217 | —237 | —252 | ||||||
| —253 | —216 | —251 | ||||||
| —228 | —228 | —206 | ||||||
| —230 | —193 | —214 | ||||||
| —201 | —234 | —227 | ||||||
| —237 | —229 | —239 | ||||||
| —221 | —210 | —196 | ||||||
| —214 | —243 | —214 | ||||||
| —257 | —251 | —279 | ||||||
| —227 | —207 | —259 | ||||||
| —269 |
Вариант 2