Временное и стационарное уравнение Шрёдингера

Волновая функция

ЛЕКЦИЯ № 9

 

Де Бройль сопоставил свободно движущейся частице плоскую волну (смысл которой сначала был не ясен).

Заменив и на р и Е уравнение волны де Бройля пишут в виде:

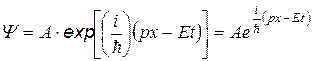
Функцию 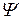называют волновой функцией, (по Борну) квадрат которой определяет вероятность 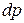нахождения частицы в пределах объема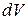

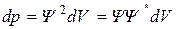
- комплексно сопряженная .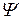

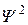- выражает плотность вероятности нахождения частицы в соответствующем месте пространства.

Интеграл по всему пространству дает 1:

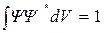- и называют условием нормировки

На 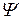- функцию налагают стандартные условия: она должна быть непрерывной, однозначной, конечной, иметь непрерывную и конечную производную.

 

Таким образом, квантовая механика имеет статистический характер, она определяет лишь вероятность нахождения частицы в данной точке пространства.

Волновая функция является решением уравнения Шрёдингера, полученным им в 1926 оду Общий вид его:

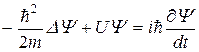(2)

m – масса частицы

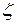- мнимая частица

U – потенциальная энергия частицы

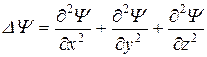- оператор Лапласа

Это уравнение не выводится и получено Шредингером из оптико-механической аналогии уравнений светового луча и траекторий движения частиц.

 

Можно придти к уравнению Шредингера следующим образом:

Пусть движется свободная частица, тогда

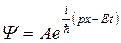
вдоль Х. (U = 0)

Тогда ;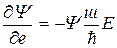

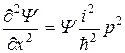
Выразив Е и р², получим:

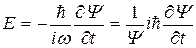
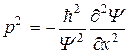
Учтя, что 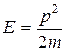, получим

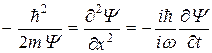
совпадает с (2) при U = 0

 

В случае, если силовое поле. В котором движется частица стационарно (U не зависит от t) то волновую функцию можно разбить на две части, зависящую от координат и времени.

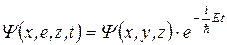
При подстановке 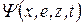во временные уравнения Шредингера (2) и после сокращения на 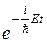придем к уравнению Шрёдингера для стационарных состояний

(3)

или

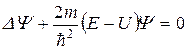
Теперь плотность вероятности

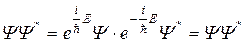
В связи с принципом неопределенности и введением волновой функции принцип причинности в квантовой механике видоизменяется. Если по силовому полю и начальным условиям решая уравнения Ньютона в классической механике мы определяем положение и скорость частицы, то в квантовой механике, зная волновую функцию и силовое поле можем найти волновую функцию при помощи уравнения Шредингера в любой момент времени.

Различие в поведении квантовых и классические частиц проявляется в том случае если на пути частицы встречается потенциальный барьер 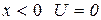(при , при )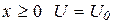

Для классической частицы: если Е – полная энергия частицы меньше U₀ то она не преодолеет и, потеряв часть скорости, будет двигаться вдоль Х.

Для квантовой частицы: если 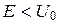,она проникнет на некоторую глубину, а затем начнет двигаться обратно.

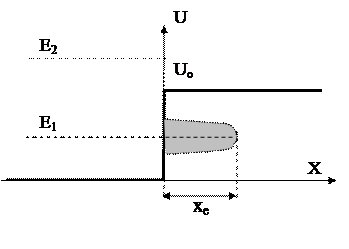Глубиной проникновения . при которой вероятность нахождения частицы уменьшается в е раз

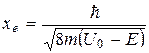
Например, металлическое тело для свободных электронов является потенциальной ямой с U₀, которая выше Е электрона на 1 эВ. Тогда Å.

Поверхность металла является потенциальным барьером, который электроны преодолевают на глубину 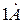и возвращаются обратно. Следовательно, поверхность металла окружена облаком электронов

Даже если , то (возможно) есть вероятность отражения частицы от барьера

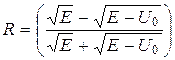
Для барьера конечной ширины вероятность того, что квантовая частица пройдет барьер называется коэффициентом прохождения (прозрачности)

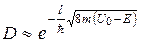
Для барьера произвольной формы

Частица как бы проходит через «туннель» в потенциальном барьере и поэтому такое явление называется туннельным эффектом.

В туннеле 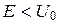получается, что кинетическая энергия отрицательна. Такого быть не может, так как одновременно знать кинетическую и потенциальную энергию в квантовой механике невозможно, то же самое, что одновременно и x, следовательно, понятие отрицательной кинетической энергии абсурдно.