Системы счисления

Известно много способов представления чисел. В каждом случае число изображается группой символов (словом) некоторого алфавита. Будем называть такие символы цифрами, символические изображения чисел ¾ кодами, а правила получения кодов ¾ системами счисления (кодирования).

Определение 1. Система счисления¾ это совокупность правил для обозначения и наименования чисел.

Системы счисления делятся на следующие виды:

1) непозиционная система счисления;

2) позиционная система счисления.

Простейшая и самая древняя ¾ так называемая унарнаясистема счисления. В ней для записи любых чисел используется всего один символ ¾ палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Сами того, не осознавая, этим кодом пользуются малыши, показывая на пальцах свой возраст. Именно унарная система счисления до сих пор вводит детей в мир счета.

Определение 2. Непозиционнойназывается такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения в коде чисел.

Непозиционные системы счисления возникли раньше позиционных. Для записи промежуточных чисел используется правило: меньшие знаки, поставленные справа от большего, прибавляются к его значению, а меньший знак, поставленный слева от большего, вычитается из него. Непозиционные системы счисления имеют ряд недостатков:

1. Для записи больших чисел приходится вводить новые цифры. И всегда есть числа, которые трудно изобразить даже вновь введенными цифрами.

2. Невозможно записывать дробные и отрицательные числа.

3. Сложно выполнять арифметические операции.

Определение 3. Системой счисления называется позиционной, если количественный эквивалент (значение) цифры зависит от ее места (позиции) в коде числа.

В привычной нам системе счисления для записи чисел используется десять различных знаков (цифры 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9). Поэтому ее называют десятичной. Имеет место не только сама цифра, но и ее позиция. Именно поэтому такую систему счисления называют позиционной. Потребовалось много тысячелетий, чтобы люди научились называть и записывать числа так, как это делаем мы с вами. Начало этому положено в древнем египте и вавилоне и было в основном завершено индийскими математиками в v- vii веках н. Э. Арабы, познакомившись с этой нумерацией первыми, по достоинству ее оценили. Получив название арабской, эта система в xii веке нашей эры распространилась по всей европе и, будучи проще и удобнее остальных систем счисления, быстро их вытеснила. Арифметические действия над десятичными числами производятся с помощью простых операций. Изучаемые в раннем возрасте, эти правила усваиваются так прочно, что мы оперируем ими подсознательно. Кроме десятичной цивилизации известны многие другие позиционные системы счисления

Основные достоинства любой позиционной системы счисления ¾ простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любого числа. Позиционная система записи чисел удобна и для механического представления чисел. Некоторый физический носитель состоит из некоторого числа n однородных элементов, каждый из которых может находиться в одном из десяти состояний. Любая такая система пригодна для изображения или записи различных чисел.

Определение 4. Основанием (базисом)позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.

Основание в любой системе записывается как 10, но в разных системах имеет разное количественное значение. Оно показывает, во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию.

Позиционных систем очень много, так как за основание системы счисления можно принять любое число не меньше двух. Наименование системы счисления соответствует ее основанию (десятичная, двоичная, пятеричная и т. Д.) В системе счисления с основанием q единицами разрядов служат последовательные степени числа q, иначе говоря, q единиц какого-либо разряда образуют единицу следующего разряда. Для записи чисел в q-ичной системе счисления требуется q различных знаков, изображающих 0, 1, 2, ... , q-1. В позиционной системе счисления любое вещественное число может быть представлено в следующем виде:

) (1)

Или (2) здесь 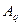¾ само число, q ¾ основание системы счисления, 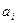¾ цифры данной системы счисления, n ¾ число разрядов целой части числа, m ¾ число разрядов дробной части числа.

Определение 5. Запись числа по формуле (1) называется развернутой формой записи.

Определение 6. Свернутой формой записичисла называется запись в виде: .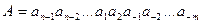

Иначе свернутую форму записи называют естественной, или цифровой.

Наряду с широко известными системами счисления, существуют смешанные системы счисления. Из всех позиционных систем счисления особенно проста и поэтому интересна двоичная система счисления. В ней для записи используются всего две цифры: 0 и 1. Основание q=2. Для двоичной системы счисления формула (1) примет вид: .

В информатике имеют большое распространение также восьмеричная и шестнадцатеричная системы счисления: использование этих систем объясняется простым переводом чисел (8=2^3, 16=2^4), что важно при выполнении записи программы, вводе данных, которые будут короче в восьмеричной или шестнадцатеричной по сравнению с двоичной системой.