Унификация
Вычислительная модель логических программ
Лекция №4
Основу вычислительной модели логических программ составляет алгоритм унификации. Унификация является основой автоматической дедукции и логического вывода в задачах искусственного интеллекта.
Терм t есть общий пример двух термов t1 и t2, если существуют такие подстановки Θ1 и Θ2, что t равно t1Θ1 и t2Θ2.Терм s называется более общим, чем терм t, если t – пример s, но s не является примером t. Терм s называется алфавитным вариантом терма t, если t – пример s и .s – пример t. Алфавитные варианты совпадают с точностью до переименования переменных, входящих в термы. Например, термы member(X,tree(Left,X, Right}) и member(Y, tree (Left,Y,Z)) являются алфавитными вариантами.
Унификатором двух термов называется подстановка, которая делает термы одинаковыми. Если существует унификатор двух термов, то термы называются унифицируемыми. Существует тесная взаимосвязь между унификаторами и общими примерами. Любой унификатор определяет общий пример, и обратно, любой общий пример определяет унификатор.
Например, append([1,2,3],[3,4],List) и append([X|Xs],Ys,[X|Zs]) унифицируемы. Унифицирующая подстановка {X = 1, Xs = [2,3], Ys = [3,4], List = [1,Zs]}. Общий пример, задаваемый этой подстановкой, – это append([1,2,3],[3,4][1|Zs]}.
Наибольшим общим унификатором, или н.о.у., двух термов называется унификатор, соответствующий наиболее общему примеру. Если два терма унифицируемы, то существует единственный наибольший общий унификатор. Единственность определена с точностью до переименования переменных. Это эквивалентно тому, что два терма имеют единственный, с точностью до изоморфизма, наибольший общий пример.
Алгоритм унификации находит наибольший общий унификатор двух термов, если такой существует. Если термы не унифицируемы, алгоритм сообщает об отказе.
Описываемый алгоритм унификации основан на решении системы равенств. Входом алгоритма являются два терма T1, и Т2. Результатом работы алгоритма является н. о. у. двух термов, если термы унифицируемы, или отказ, если термы не унифицируемы. Алгоритм использует стек для хранения равенств, подлежащих решению, и ячейку памяти Θ для построения выходной подстановки. В начале работы ячейка Θ пуста, в стек помещается равенство T1=Т2. Алгоритм состоит из цикла, в теле которого из стека считывается и обрабатывается одно равенство. Цикл завершается, если в процессе работы появляется сообщение об отказе или стек оказывается пустым.
Рассмотрим возможные действия при считывании равенства S = Т. Простейший случаи, когда S и Т – одинаковые константы или переменные. Тогда равенство корректно, и ничего делать не надо. Вычисление продолжается, из стека считывается следующее равенство.
Если S – переменная, а T – терм, не содержащий вхождений S, то происходит следующее.В стеке отыскиваются все вхождения переменной S и каждое из них заменяются на T. Аналогично все вхождения S в Θ заменяются на Т. Затем подстановка S=T добавляется к Θ. Существенно, что S не входит в Т. Проверка, соответствующая словам «не содержит вхождений», известна как проверка на вхождение.
Если T – переменная, S – терм, не содержащий Т, т. е. T удовлетворяет проверке на вхождение относительно выполняется аналогичная последовательность действий.
Равенства добавляются в стек, если S и T – составные термы с одним и тем же главным функтором одной и той же арности арности, например: f(S ,.., S
,.., S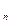 ,) и f(T
,) и f(T ,…, T
,…, T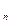 ). Для унификации термов следует совместно унифицировать каждую пару аргументов, что достигается помещением в стек n равенств вида S
). Для унификации термов следует совместно унифицировать каждую пару аргументов, что достигается помещением в стек n равенств вида S =Т
=Т .
.
Во вcех остальных случаях выдается сообщение об отказе, и работа алгоритма завершается. Если стек пуст, то термы унифицируемы и унификатор содержится в Θ. Полный алгоритм приведен на рис. 4.1. Фраза «не входящая в» подразумевает проверку на вхождение.
Мы не доказываем корректность алгоритма и не анализируем его сложность.
Вход: Два терма Т , и T
, и T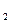 , которые надо унифицировать.
, которые надо унифицировать.
Результат: Подстановка Θ – н.о. у. Т , и T
, и T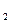 термов или отказ.
термов или отказ.
Алгоритм:
Начальное значение подстановки Θ пусто, стек содержит равенство Т =T
=T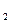 ,
,
failure := false, пока стек не пуст и не failure, выполнить.
считать Х = Y из стека
ветвление
Х – переменная, не входящая в Y:
заменить все вхождения Х в стеке и в Θ на Y
добавить Х = Y к Θ
Y – переменная, не входящая в X:
заменить все вхождения Y в стеке и в Θ на Х
добавить Y= Х к Θ
Х и Y – одинаковые константы
или переменные:
продолжать
Х естьf(X ,...,X
,...,X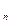 ) и Y есть
) и Y есть
f(Y ,...,Y
,...,Y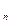 )
)
для некоторого функтора f и п> 1:
поместить X == Y
== Y для всех i=1, ..., п в стек
для всех i=1, ..., п в стек
в остальных случаях:
failure :== true
если failure, то результат – отказ;
иначе результат Θ.
Рис. 4.1. Алгоритм унификации.
Рассмотрим попытку унификации термов append([a,b],[c,d],Ls) и append([X | Xs], Ys, [X | Zs]). Начальное состояние стека:
append([a,b],[c,d]Ls) = append([ Xs| Ys,[X | Zs]).
Эти два терма имеют один и тот же функтор – append одной арности 3, поэтому в стек добавляются три равенства, соответствующие подтермам двух термов:
[a,b] = [X|Xs],[c,d] = Ys и Ls = [Х|Хs].
Следующее равенство [а, b] = [X|Xs] считывается из стека. Эти два составных терма имеют один и тот же функтор «•» арности 2, поэтому в стек добавляются два равенства а = Х и [b] = Xs. Далее считывается равенство a = X. Ситуация совпадает со второй ветвью алгоритма на рис. 4.1. Х –переменная, не входящая в константу а.Все вхождения Х в стеке заменяются на а. Одно равенство при этом изменяется, а именно: Ls = [X | Zs] превращается в Ls = [a | Zs]. Равенство Х =a добавляется к начально пустой подстановке, и работа алгоритма продолжается.
Считывается следующее равенство: [b] = Xs. Вновь работает вторая ветвь алгоритма. Равенство Xs = [b] добавляется к множеству подстановок, стек проверяется на вхождения Xs. Таких вхождений нет, считывается следующее равенство.
Все та же вторая ветвь используется и для равенства [c,d] = Уs. Новая подстановка Ys = [с, d] добавляется к имеющимся, и считывается последнее равенство Ls = [а | Zc], Здесь применима симметричная первая ветвь алгоритма.Ls не входит в [a | Zs], так что равенство добавляется к унификатору и алгоритм успешно завершает работу. Унификатором является подстановка {X = a,Xs = [b],Уs = [c,d],Ls=[a | Zs]}. Общий пример, полученный с помощью унификатора, – аррend([a,b][c,d],[a |Zs]). Заметим, что при данной унификации в процессе работы подстановки не изменялись.
Проверка на вхождение необходима, чтобы предотвратить попытку унифицировать такие термы, как s{X} и X. Эти термы не имеют конечного общего примера.
При реализации алгоритма унификации в конкретных языках программирования явных подстановок в равенства, размещенные в стеке, и в унификатор избегают. Вместо этого логические переменные и другие термы представляются ячейками памяти с различными значениями, и связь с переменной обеспечивается ссылкой из ячейки памяти, представляющей логическую переменную, на ячейку памяти, содержащую представление терма, связанного с переменной. Таким образом, вместо
заменить все вхождения Х и У в стеке и в Θ
добавить Х = Y к подстановкам
используется
построить в Х ссылку на Y.