Основные понятия теории формальных языков и грамматик

Выводы цепочек формального языка. Деревья КСГ

Старый дуб заслоняет старый дом

 

Дерево представляет собой синтаксическую структуру предложения. Из него видно, что результирующая цепочка не зависит от порядка, в котором делались замены промежуточных элементов. Элементы грамматики, такие как подлежащее, существительное и другие, называются вспомогательными или нетерминальными символами. В контекстно-свободной грамматике может быть любое конечное число нетерминальных символов. Символы - дуб, дом, старый, заслоняетв рассмотренной грамматике играют роль слов из словаря языка и называются терминальными (основными) символами или просто терминалами. Может существовать любое конечное число терминалов в контекстно-свободной грамматике. В языках программирования терминальными являются используемые в них слова и символы: DO, IF, + и др.

В общем виде правила грамматики можно записать:

нетерминал ® любая конечная цепочка терминальных и нетерминальных символов или одних терминалов.

Цепочка справа от стрелки может быть пустой, что обозначается в

грамматике следующим образом: < F> ® e. Такое правило называется эпсилон - правилом.

В отдельных языках программированияправилавыглядят в соответствии с записью:

 

< оператор > ® IF < логическое выражение > THEN < оператор >

 

Один из нетерминальных символов всегда выделяется в качестве начального. Его называют аксиомой грамматики. С него всегда должен начинаться вывод цепочек языка.

Контекстно-свободная грамматика (КСГ) задается:

конечным множеством терминалов; - конечным множеством нетерминалов; конечным множеством правил вида < A > ® a, где А - нетерминал, a - цепочка терминальных и нетерминальных символов ( возможно пустая ) или цепочка терминальных символов; нетерминал А называется левой частью правила, а a - правой; одним нетерминальным символом, выделенным в качестве начального (аксиомой грамматики).

Проанализируем грамматику, правила которой имеют вид:

 

1. S ® a A b S 2. S ® b

3. A ® A S c 4. A ® e

 

Из записи следует: { A,S } - словарь нетерминальных символов;

{a, b, c} - словарь терминальных символов; e - пустая цепочка и, следовательно, не является символом грамматики. Правило 4 можно записать в виде А ®. Аксиома грамматики – символ S.

Рассмотрим еще один способ записи правил формальной грамматики, называемый формой Бэкуса-Наура:

 

1. <S>:= a <A> b <S> | b 2. <A>:= <A> <S> c | e

 

 

Правила грамматики задают способы подстановки цепочек. Подстановка осуществляется заменой нетерминального символа в заданной цепочке на правую часть правила, левой частью которого является такой нетерминал.

Рассмотрим грамматику с аксиомой грамматики < S > и правилами вывода вида:

1. S ® a A B c 2. S ® e 3. A ® c S B

4. A ® A b 5. B ® b B 6. B ® a

Если начать вывод цепочек языка, используя первое правило, то последовательность подстановок может быть следующей:

· S® a A Bc ( 1 правило )

· S® a A b B c ( 5 правило )

· S® a A b b a c ( 6 правило )

· S® a c S B b b a c ( 3 правило )

· S® a c S a b b a c ( 6 правило )

· S ® a c e a b b a c ( 2 правило )

В рассмотренном выводе присутствует семь цепочек, включая начальную и заключительную.

 

Определение. Язык, задаваемый грамматикой, есть множество терминальных цепочек, которые можно вывести из начального символа грамматики.

 

Построим дерево вывода цепочки: a c a b a c , используя выше рассмотренную грамматику.

 

S

 

aA B c

 

A b a

c S B

 

e a

 

Замечание. Для каждого дерева существует единственный левый и правый выводы, то есть вывод, когда на каждом шаге заменяется самый левый (правый) нетерминальный символ. Многие методы обработки языков рассчитаны исключительно на левый (правый) выводы. В подобных случаях пишут:

a ® _LB (L - left)

a ® _RB (R - right ).

 

Цепочке языка может соответствовать более чем одно дерево, так как она может иметь разные выводы, порождающие разные деревья. Если одна цепочка имеет несколько деревьев вывода, то говорят, что соответствующая грамматика неоднозначна.

 

Пусть задан алфавит V терминальных символов. Множество всех конечных слов или цепочек в алфавите V обозначим V*.

Формальный язык Lнад алфавитом V - это подмножество множества V*,то есть L (V) Í V*[ 3 ].

Конструктивное описание формального языка осуществляется с помощью формальных систем, называемых формальными порождающими грамматиками.

Определение. Формальной порождающей грамматикой G называется формальная система, описываемая с помощью четырех формальных объектов

{ V, W, P, S }, где V - словарь терминалов, W - словарь нетерминалов, причем VÇ W = Æ, P - множество правил вида j ® y, где j и y Î ( V È W ),

S - аксиома грамматики.

 

Определение.Цепочка b называется выводимой из цепочки a, если они представимы в виде:

b= l j d a= l y d

и в грамматике существует правило вида y ® j.

 

Определение. Цепочка b называется выводимой из a, если существует конечная последовательность цепочек вывода:

a ® x₀ x₀ ® x_{1, ...,} x_k ® b , где цепочка x_i непосредственно выводима из x_i-1 для всех i = 0,1,..., k-1.

Введем обозначение a ® b. Это значит, что b выводима из a

в грамматике G.

 

Определение. Языком L(G), порождаемым грамматикой G, называется множество всех цепочек, выводимых из аксиомы грамматики.

 

Определение. Грамматики G1 и G2 эквивалентны тогда и только тогда, когда они порождают один и тот же язык.

 

Классификация грамматик Холмского

Тип 0 - грамматика произвольного вида без ограничений на правила вывода.

Тип 1 - контекстная грамматика. Контекстная грамматика, правила которой имеют вид:

a A b ® a w b, A Î W*, w Î (V È W)*,

где w - непустая цепочка, a и b - контекст правила ( цепочки символов, которые не заменяются и не изменяются при его применении).

Тип 2 - контекстно-свободная грамматика (КСГ), правила которой имеют вид

A ® a, a Î (V È W)*.

Тип 3 - регулярная грамматика, все правила которой имеют вид:

A ® a B

A ® a, a Î V, B Î W.

 

Определение. Язык, порождаемый грамматикой определенного типа , называют языком такого же типа.

 

Пример. Определить тип языка, цепочки которого имеют вид

 

{ a, aaa, aaaaa ... a^2n-1 .... }.

 

Решение. Определим объекты грамматики и определим ее правила, позволяющие строить цепочки заданного языка. Ими будут:

 

V = {a}, W = {S}, P = { S ® a a S, S ® a }.

 

Из всего следует, что это язык типа 2.

Пример.Определить тип языка булевых функций.

 

Решение.Грамматику зададим объектами:

G = {V, W, P, S}, V= { a, b, c, &, È, Ø, (, ) }, W = {S},

и правилами вида:

 

1. S ® ( S & S ) 4. S ® a

 

2. S ®( S È S ) 5. S ® b

 

3. S ® Ø S 6. S ® c.

 

 

Анализ показывает, что это контекстно-свободная грамматика,

и язык, порождаемый ей, есть язык типа 2.

 

Пример.Определить тип языка, цепочки которого имеют вид

{ a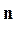b}.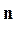

 

Решение.Запишем правила, с помощью которых можно вывести цепочки заданного языка. Они имеют вид:

 

S ® a S b; S ® a b.

 

Как показывает анализ, заданный формальный язык принадлежит типу 2.