Программная реализация логических функций и автоматов

F1

Представление автомата схемой, состоящей из логических элементов наиболее исследованный вид структурной реализации автомата. Другой ее вид - реализация программой. Программа вычисляет (реализует) логические функции f(x_1, ..., x_n) = y, если для любого двоичного набора d = ( d₁,..., d_n ) при начальном состоянии элементов памяти x₁ = d₁ , x₂ = d₂ ,..., x_n = d_n программа через конечное число шагов останавливается и в ячейке y лежит величина f(d1, d2, ..., dn ). Если под сложностью схемы, реализующей автомат, обычно понимается число элементов схемы, то под сложностью программ можно понимать:

n число команд в тексте программы;

n объем промежуточной памяти;

n время вычисления программы, которое характеризуется двумя величинами:

1. Средним временем

2. Максимальным временем ,

где сумма и максимум берутся по всем 2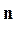наборам, а t_p - время работы программы на одном наборе s.

Рассмотрим 2 типа программ: операторные и бинарные. Операторная программа не содержит условных переходов, порядок ее команд в точности соответствует нумерации элементов в схеме, а система команд соответствует базису схемы. Элементы схемы нумеруются числами 1,..., n таким образом, чтобы на любом пути от входа к выходу номера элементов возрастали. При этом номер 1 получит один из входных элементов, а номер n - выходной элемент.

Пусть элемент схемы e_i реализует функцию j_i и к его входам присоединены выходы элементов e_j1 , e _j2 , ..., e _jm (некоторые из них, возможно, являются входами схемы ), тогда выход такого элемента можно записать:

a_i = j_i ( e_j1 , e _j2, ..., e _jm ) при i ¹ n, а выход схемы может быть записан: y = j_i( e_j1, e _j2, ..., e _jm ) при i = n. Такая программа будет реализовывать работу заданной схемы. Проблема синтеза операторных программ сводится к проблеме синтеза схем, то есть к вопросам функциональной полноты и минимизации схем. Поскольку операторная программа не содержит условных переходов, то время ее выполнения на любом наборе одно и то же, отсюда

t _max = t _ср.

Бинарные программы это программы, состоящие из команд типа y = d; d = {0, 1} и условных переходов.

 

Замечание. Бинарные программы обладают двумя достоинствами по сравнению с операторными:

1. Отсутствием промежуточной памяти в процессе работы программы. Это позволяет реализовать бинарную программу на постоянных элементах памяти.

2. Более высоким быстродействием.

 

Пример. Составить для функции f = x1 v Øx2 бинарную и операторную программы.

 

Решение. Воспользуемся языком С++, будем иметь код:

void main()

{

bool f=0, x1,x2 ; // описание типа переменных

 

cout<<” Enter x1,x2\n”; // вывод на экран текста

cin>> x1>>x2; // ввод переменных

 

switch (x1) // оператор выбора

{

case 0: switch(x2)

{

case 0: f=1;

case 1: f=0;

}

case 1: f=1;

}

 

default: f=0;

cout>> ”\n f = “<<f ;

getch();

 

}

 

 

Операторная программа пишется в базисе {&,Ø}. Для этого перепишем заданную функцию, используя формулы де Моргана.

 

void main()

{

 

bool f, x1,x2 ; // описание типа переменных

bool a,b;

 

cout<<” Enter x1,x2\n”; // вывод на экран текста

cin>> x1>>x2; // ввод переменных

 

a= 1-x1; {}

b= a * x2; {}

b= 1 - b; {}

f=b;

 

cout>> ”\n f = “<<f ;

getch();

}

 

Контрольный вопрос.Определить к какому типу программ относится программа, фрагмент которой представлен оператором:

 

f = (x1) OR ( NOT (x3)) AND ((x5) AND (NOT (x4)));