Ускорители заряженных частиц

Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и на­правляются пучки высокоэнергетических заряженных частиц (электронов, про­тонов, мезонов и т.д.).

Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка Ускорители делятся на непрерывные (из них частицы вылетают порциями - им­пульсами). Последние характеризуются длительностью импульса. Но форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индук­ционных траекториями частиц являются окружности или спирали.

Рассмотрим некоторые типы ускорителей заряженных частиц.

1. Линейный ускоритель. Ускорение частиц осуществляется
электростатическим полем. Заряженная частица проходит поле однократно за­ряд Q, проходя разность потенциалов , приобретает энергию . Таким способом частицы ускоряются до10МэВ. Их дальнейшее ускорение с помощью источников постоянного напряжения невозможно из-за утечки зарядов, пробоев и т.д.

2. Циклотрон - циклический резонансный ускоритель тяжелых частиц (протонов, ионов). Его принципиальная схема приведена на рис. 41.

Рис. 41

Между полюсами электромагнита помеща­ется вакуумная камера, в которой находятся два электрода (1 и 2) в виде полых металли­ческих полуцилиндров, или дуантов. К дуантам приложено переменное электрическое поле. Магнитное поле, создаваемое элек­тромагнитом, однородно и перпендикулярно плоскости дуантов.

Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полем, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменяется, поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокруж­ность большего радиуса и т. д.

Для непрерывного ускорения частицы в циклотроне необходимо выпол­нить условие синхронизма: периоды вращения частицы в магнитном иоле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допус­тимых значений, пучок частиц посредством отклоняющего электрического по­ля выводится из циклотрона.

Циклотроны позволяют ускорять протоны до энергии примерно 20МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским воз­растанием массы со скоростью, что приводит к увеличению периода вращения, и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при Е=0,5МэВ, m=2m₀; при Е=10МэВ, m=28m₀).

Ускорение релятивистских частиц в циклических ускорителях можно, од­нако, осуществить, если применить предложенный в 1944г. советским физиком В.И.Векслером и в 1945г. американским физиком Э.Мак-Милланом прин­цип автофазировки. Его идея заключается в том, что для компенсации увеличения периода вращения частиц, ведущего к нарушению синхронизма, изменяют либо частоту ускоряющего электрического поля, либо индукцию магнитного поля, либо то и другое. Принцип автофазировки используется в фа­зотроне, синхротроне и синхрофазотроне.

 

3.9. Циркуляция вектора для магнитного поля в вакууме

 

Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Цирку­ляцией вектора по заданному замкнутому контуру называется интеграл

,

где 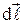- вектор элементарной длины контура, направленной вдоль обхода кон­тура. cosα - составляющая вектора в направлении касательной к конту­ру, α - угол между векторами и .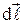

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора ) читается так: циркуляция вектора по произвольному замкнутому контуру равна произведению магнитной постоянной μ₀ на алгебраическую сумму токов, захватываемых этим контуром:

, (3.18)

где n - число проводников с током, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается кон­туром. Положительным считается ток, направление которого связано с направ­лением обхода по контуру правилом правого вита, ток противоположного на правления считается отри нательным. Например, для системы токов, изобра­женных на рис. 42,

.

Выражение (3.18) справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.

Продемонстрируем справедливость теоремы о циркуляции вектора на примере магнитного поля прямого тока I, перпендикулярного плоскости черте­жа и направленного к нам (рис.43).

Рис. 42 Рис. 43

Представим себе замкнутый контур в виде окружности радиуса R. В каж­дой точке этого контура вектор одинаков по модулю и направлен по каса­тельной к окружности. Следовательно, циркуляция вектора равна

.

Согласно выражению (3.18), получим , откуда

.

Таким образом, исходя из теоремы о циркуляции вектора , получили вы­ражение для магнитной индукции поля прямого тока, выведенное выше см.(3.7).

Сравнивая выражения (1.14) и (3.18) для циркуляции векторов и , ви­дим, что между ними существует принципиальное различие. Циркуляция век­тора электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляция вектора магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, т.к. позволяет находить маг­нитную индукцию поля без применения закона Био-Савара-Лапласа.