Электростатических полей в вакууме
Применение теоремы Гаусса к расчету некоторых
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость (рис.8) заряжена с постоянной поверхностной плотностью +σ ( – заряд, приходящийся на единицу поверхности). – заряд, приходящийся на единицу поверхности).
|
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей.
Так как образующие цилиндра параллельны линиям напряженности (cosα=0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания (площади оснований равны, и для основания En совпадает с Е), т.е. 2ES. Заряд, заключенный внутри построенной цилиндрической поверхности, равен σS. Согласно теореме Гаусса, 2ES=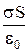 .
.
Откуда
 . (1.8)
. (1.8)
Из формулы (1.8) вытекает, что Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
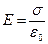 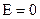   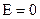  Рис. 9
Рис. 9
| 2. Поле двух бесконечных параллельных разноименно заряженных плоскостей (рис.9).
В области между плоскостями Е=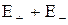 ( ( и и  определяются по формуле (1.8)), поэтому результирующая напряженность определяются по формуле (1.8)), поэтому результирующая напряженность
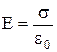 . (1.9) . (1.9)
|
Таким образом, результирующая напряженность поля и области между плоскостями описывается формулой (1.9), а вне объема, ограниченного плоскостями, равна нулю.
3. Поле равномерно заряженной сферической поверхности.
Сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью σ+.
Благодаря равномерному распределению заряда по поверхности поле, создаваемое им, обладает сферической симметрией. Поэтому линии напряженности направлены радиально (рис.10).
 Рис. 10 Рис. 10
| Построим мысленно сферу радиусом r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд Q, создающий рассматриваемое поле, и, по теореме Гаусса,  .
Откуда .
Откуда
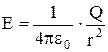 (r≥R). (1.10) (r≥R). (1.10)
|
При r > R поле убывает с расстоянием r по такому же закону, как у точечного заряда. График зависимости Е от r приведен на рис. 11.
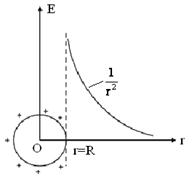 Рис. 11
Рис. 11
| Если r < R, то замкнутая поверхность не содержит внутри зарядов, поэтому внутри равномерно заряженной сферической поверхности электростатическое поле отсутствует (Е=0). |

 4. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 12) заряжен равномерно с линейной плотностью τ (
4. Поле равномерно заряженного бесконечного цилиндра (нити). Бесконечный цилиндр радиуса R (рис. 12) заряжен равномерно с линейной плотностью τ (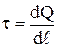 - заряд, приходящийся на единицу длины).
- заряд, приходящийся на единицу длины).
Для расчета напряженности электростатического поля в точке, отстоящей на расстоянии r от оси цилиндра (см. рис.12) или нити, можно воспользоваться формулой (1.11).
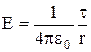 (r≥R). (1.11)
(r≥R). (1.11)
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е=0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (1.11), внутри же его поле отсутствует.