Модель частичной (неполной) корректировки
Если в моделях учитывают не фактическое значение переменной, а ее желаемое (ожидаемое) значение, то такие модели относят ко 2-му типу динамических эконометрических моделей – моделям ожиданий, либо к моделям частичной (неполной) корректировки.
Модель частичной корректировки (МЧК) учитывает желаемое (ожидаемое) значение результативного признака 
. Примером МЧК может служить модель Литнера: фактический объем прибыли хt оказывает влияние на величину желаемого объема дивидендов . В общем виде модель частичной корректировки можно записать так:
. (3.10)
Желаемое (ожидаемое) значение переменных определяется по значению реальных (фактических) переменных в предыдущий период времени t - 1.
В таких моделях предполагается, что фактическое при ращение зависимой переменной 
пропорционально разнице между ее желаемым уровнем и фактическим значением в предыдущий период 
:
или 
(3.11)
(21)
Из этого следует, что уt получается как среднее арифметическое взвешенное желаемого уровня и фактического значения этой переменной в предыдущем периоде уt-1. Чем больше величина l, тем быстрее происходит процесс корректировки. Если значение l. = 1, то 
и полная корректировка происходит за 1 период. Если l = 0, то корректировка уt не происходит совсем.
Подставив (3.10) в (3.11) получим:
.
Параметры преобразованного уравнения регрессии а, l, b0 могут быть оценены с помощью обычного МНК. Данная модель, как и в методе Койка (см. п. 3.6.3) включает стохастическую объясняющую переменную уt-1. Но теперь эта переменная не коррелирует с текущим значением совокупного случайного члена (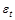 
) уравнения (поскольку vt, так же как и иt, рассчитывается после того, как определилось значение уt-1). При таких условиях обычный МНК позволяет получать асимптотически несмещенные и эффективные оценки (исключение составляют малые выборки).
Соотношение: 
включает только фактические значения переменных, его еще называют краткосрочной функцией МЧК.
Исходное уравнение (3.10) называют долгосрочной функцией МЧК.
Тесты по разделу