Автокорреляция случайных составляющих. Обнаружение автокорреляции случайных составляющих. Критерии Дарбина-Уотсона

Автокорреляция – корреляционная зависимость между текущими уровнями некоторой переменной и уровнями этой же переменной, сдвинутыми на несколько периодов времени назад.

Автокорреляция случайной составляющей u – корреляционная зависимость текущих u_i и предыдущих u_i_-_L значений случайной составляющей. Величина L называется запаздыванием, сдвигом во времени или лагом. Лаг определяет порядок автокорреляции.

Автокорреляция случайной составляющей нарушает 4-ю предпосылку нормальной линейной модели регрессии: 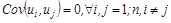(условие независимости случайных составляющих в различных наблюдениях, i,j – номера наблюдений).

Наличие случайной составляющей u_i в уравнении регрессии может быть обусловлено: невключением в уравнение регрессии объясняющих переменных (неучтенными факторами); агрегированием переменных; неправильной функциональной спецификацией модели; ошибками измерения.

Обычно автокорреляция встречается при использовании данных временных рядов. Допустим, что случайная составляющая обусловлена только невключением в модель объяс няющих переменных. Тогда, если значение u_i в i-м наблюдении должно быть независимым от его значения в предыдущем (i – L)-м наблюдении u_i_-_L, то и значение любой факторной переменной, «скрытой» в u, должно быть некоррелированным с ее значением в предыдущем наблюдении.

Рассмотрим пример автокорреляции случайных составляющих (взятый из учебника Доугерти [6]). Проанализируем модель зависимости спроса на мороженое у от дохода х (учтенный фактор). На у оказывают влияние не только доход х, но и другие факторы, которые не учтены в модели. Допустим, что один из таких факторов – время года. Летом спрос на мороженое выше, чем зимой. Данный фактор находит свое отражение в случайной составляющей.

Автокорреляция может быть как положительной, так и отрицательной.

Положительная автокорреляция означает постоянное в одном направлении действие неучтенных факторов на результат. Например, спрос на мороженое всегда выше линии тренда летом (т. е. для летних наблюдений u > 0) и ниже зимой (т. е. для зимы u < 0) (рис. 2.4).

X(доход)

Рис. 2.4. Пример положительной автокорреляции

Отрицательная автокорреляция означает разнонаправленное действие неучтенных в модели факторов на результат, что приводит к отрицательной корреляции между последовательными значениями случайной составляющей. То есть за положительными значениями случайной составляющей и в одном наблюдении следуют отрицательные значения и в следующем, и наоборот. Заметим, что отрицательная автокорреляция в экономике встречается относительно редко.

Последствия автокорреляции случайной составляющей:

• коэффициенты регрессии становятся неэффективными, хоть и несмещенными и состоятельными;

• стандартные ошибки коэффициентов регрессии становятся заниженными, а значения t-критерия завышенными.

Обнаружение автокорреляции случайной составляющей. Оценкой случайной составляющей является остаток – разность между фактическим и рассчитанным по оцененному уравнению регрессии значениями признака-результата. Так как автокорреляция случайных составляющих имеет место, в основном, когда исходные данные являются временными рядами, обозначим номер наблюдения как t (t = 1; n). Тогда для t-го наблюдения остаток будет равен: 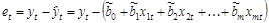, где 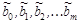– МНК- оценки коэффициентов истинного уравнения регрессии – .

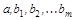Рассмотрим способы обнаружения автокорреляции остатков (а следовательно, и случайных составляющих).

Рис. 2.5. Обнаружение автокорреляции остатков

1-й способ – визуальный (графический). С помощью МНК оценивается регрессия 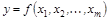. Рассчитываются остатки е_i. Строится график зависимости остатков е_t от номера наблюдения – t (t = 1; n). (рис. 2.5).

2-й способ – основан на применении критерия Дарбина-Уотсона.

Данный метод применяют для обнаружения автокорреляции, подчиняющейся авторегрессионному процессу 1-го порядка: 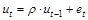(t = 1; n).

Предполагается, что величина е_t в каждом t-м наблюдении не зависит от его значений во всех других наблюдениях. Если 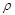положительна, то автокорреляция положительна, если 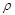отрицательна, то автокорреляция отрицательна. Если 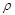= 0, то автокорреляции нет (т. е. четвертая предпосылка нормальной линейной модели выполняется).

Критерий Дарбина-Уотсона сводится к проверке гипотезы:

• Н0 (основная гипотеза): 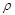= 0

• Н1 (альтернативная гипотеза): 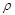> 0 или 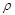< 0.

Для проверки основной гипотезы используется статистика критерия Дарбина-Уотсона – DW:

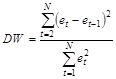, где .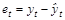

На больших выборках 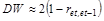, где выборочный коэффициент автокорреляции 1-го порядка.

Если , то DW = 0. Если , то DW = 4. Если 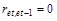, то DW = 2.

Данная статистика имеет распределение Дарбина-Уотсона. Существуют специальные статистические таблицы для определения нижней и верхней критических границ DW-статистики – d_L и d_u. Они определяются в зависимости от n и числа степеней свободы (h – 1), где h – число оцениваемых параметров.

Если 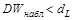, то принимается гипотеза
Н1: (положительная автокорреляция).

Если 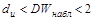, то принимается гипотеза Н0: (автокорреляции нет).

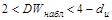Если ,то принимается гипотеза Н1: 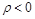(отрицательная автокорреляция).

Если , , то имеет место случай неопределенности.

Графически тест Дарбина-Уотсона представлен на рис. 2.6 (штриховкой отмечена область неопределенности):

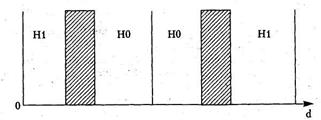
Рис. 2.6. Тест Дарбина-Уотсона на автокорреляцию

Ограничения применения DW-статистики:

• данный критерий неприменим к моделям авторегрессии: ;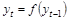

• данный критерий проверяет только гипотезу о наличии автокорреляции первого порядка;

• достоверные результаты получаются только на больших выборках.

Вместе с тем встречаются случаи, когда целесообразно предположить, что случайные составляющие связаны авторегрессионным процессом более высокого порядка L:

Например, автокорреляция 4-го порядка может иметь место при использовании в качестве данных ежеквартальных наблюдений (когда сезонные колебания переходят из года в год).

Возможны случаи, когда случайные составляющие связываются не авторегрессионным процессом, а процессом скользящих средних:

Для обнаружения автокорреляции высокого порядка используют различные методы. Рассмотрим один из них – метод Лагранжа.

Суть данного подхода заключается в следующем.

1. Решают вопрос о величине L – максимальной величине запаздывания во времени.

2. С помощью МНК оценивается исходная регрессия: 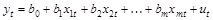и рассчитываются остатки e_t.

3. Оценивается регрессия: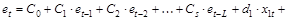

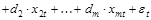
где 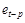– остаток в наблюдении (t-р) (р = 1; L) (t = 1; n)

x_j (j = 1; m) – объясняющие переменные первоначальной регрессии;

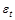– случайная составляющая для данной зависимости.

Регрессия оценивается по данным для периодов от (L + 1) до n, так как величины 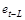не определены для первых L периодов .

4. Выдвигается основная гипотеза Н0: автокорреляция отсутствует. Для ее проверки вычисляется статистика: , которая имеет распределение 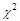(«хи-квадрат») с L степенями свободы. Определяется критическое значение 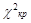, по соответствующим статистическим таблицам. Фактическое значение 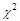сравнивается с критическим 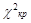. Если 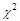> 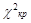, то гипотезу об отсутствии автокорреляции отвергают. Если 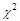< 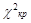, то гипотезу об отсутствии автокорреляции не отвергают.

Данный тест рассчитан на работу с большими выборками, поэтому нужно проявлять осторожность при толковании результатов, полученных на малых выборках.