Уравнение линейной регрессии

 

Если между величинами х и у установлена линейная статистическая зависимость, то представляет интерес найти ее выражение в виде уравнения прямой линии у = ах + b (где а и b – коэффициенты).

Такое уравнение называется уравнением регрессии. Если величина х неслучайная, то существует одно уравнение регрессии. Если обе величины (х и у) случайные, то имеется два уравнения регрессии и можно вычислять зависимости как у от х, так и х от у.

Расчет уравнения сводится к определению наиболее вероятного значения у, когда известно значение х. Опуская вывод, запишем уравнение линейной зависимости через статистические характеристики:

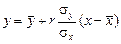. (3.12)

Аналогичный вид имеет второе уравнение зависимости х от у:

. (3.13)

Эти уравнения пересекаются в точке средних значений и , и в них входят пять статистических характеристик.

Как указывалось, дисперсия случайной величины является характеристикой ее рассеяния около математического ожидания или среднего значения. Уравнение регрессии (3.12) позволяет определить еще одну остаточную дисперсию s_d, которая характеризует рассеяние значений случайной величины около линии регрессии:

(3.14)

где d_i – отклонения значений случайной величины у от линии регрессии.

Дисперсии и 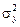связаны между собой соотношением

. (3.15)

Разность между ними также является дисперсией, учтенной (поглощенной) уравнением регрессии. Она называется дисперсией тренда или дисперсией закономерной изменчивости, противопоставляя случайной остаточной дисперсии.

Между тремя дисперсиями существует соотношение

, (3.16)

которое можно рассматривать как разложение дисперсии 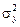на две составляющие – закономерную и случайную. Если принять дисперсию 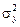за 100 %, то дисперсии тренда и остаточную можно выразить в процентах от нее.

Уравнение линейной регрессии позволяет решать несколько практических задач.

Первое назначение уравнения описательное, потому что часто важен сам факт линейной зависимости и ее аналитическое выражение.

Но наибольшая эффективность уравнения заключается в возможности прогнозирования значения одной случайной величины, если известно значение другой.

Поскольку зависимость носит статистический характер, прогнозирование по уравнению (3.12) будет сопровождаться погрешностью ts_d или, учитывая формулу (3.15), погрешностью где t – коэффициент вероятности.

Чем больше коэффициент корреляции по абсолютной величине, тем меньше погрешность прогнозирования. Для надежного прогнозирования необходимо использовать лишь такие зависимости, у которых коэффициент корреляции больше 0,87.

Пример 2. По условиям примера 1 необходимо рассчитать уравнение зависимости содержания железа магнетитового у от содержания железа общего х в руде.

По данным табл.3.1

или после раскрытия скобок у = 1,080х – 11,0. При t = 2 погрешность прогнозирования по уравнению . Поэтому можно записать у = 1,080х – 11,0 ± 5,4.

Из табл.3.1 имеем дисперсию 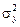= 201,32; остаточную дисперсию = 201,32(1 – 0,982²) = 7,18; дисперсию тренда = 201,32 – 7,18 = 194,14. Приняв 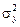за 100 %, найдем, что дисперсия тренда составит 96,4 %, а остаточная дисперсия отклонений равна 3,6 % от общей дисперсии.

Линию полученного уравнения можно нанести на график (рис.3.2). Она пересечет ось абсцисс при значении х = 11,0/1,080 = 10,2 %, что указывает на вероятное среднее содержание железа в немагнитных минералах руды. В качестве второй точки для проведения линии регрессии можно использовать средние значения = 37,1 и = 29,1.

 

 

Следует отметить, что существует и второе уравнение зависимости х от у, оно имеет вид

или х = 0,893у + 11,1, его погрешность 4,9. Линии обоих уравнений пересекаются в точке средних значений и .