Пример выявления аномальных значений
Таблица 2.6
| Номер пробы n | Значения х | Квантиль t | Номер пробы n | Значения х | Квантиль t |
| 0,06 | -2,07 | 0,49 | 0,05 | ||
| 0,15 | -1,57 | 0,50 | 0,15 | ||
| 0,21 | -1,30 | 0,52 | 0,24 | ||
| 0,25 | -1,10 | 0,53 | 0,34 | ||
| 0,28 | -0,94 | 0,57 | 0,45 | ||
| 0,29 | -0,80 | 0,60 | 0,56 | ||
| 0,32 | -0,67 | 0,64 | 0,67 | ||
| 0,35 | -0,56 | 0,67 | 0,80 | ||
| 0,38 | -0,45 | 0,73 | 0,94 | ||
| 0,39 | -0,34 | 0,75 | 1,10 | ||
| 0,42 | -0,24 | 0,80 | |||
| 0,45 | -0,15 | 1,14 | 1,57 | ||
| 0,47 | -0,05 | 1,19 | 2,07 |
Вначале найдем среднее и дисперсию из всех 26 значений: 
= 0,502; s2 = 0,06478; s = 0,2545. Далее вычислим среднее и дисперсию из 24 значений, исключив максимальные значения.
Получим смещенные оценки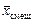 
= 0,451; 
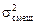= 0,03577; s = 0,1891. Вычислим нормированные значения исключенных значений: t25 = (1,14 – 0,451)/0,1891 = 3,64; t26 = (1,19 – 0,451)/0,1891 = 3,91. Поскольку нормированные значения t25 > 3 и t26 > 3, по правилу «трех сигм» оба исключенных значения являются аномальными.
Однако полученный вывод является некорректным, так как он построен на смещенных оценках.
Оценим размер смещения, обусловленный исключением двух максимальных значений. Имеем p = 1 – n/N = 0,923. Вероятности p соответствует квантиль
t = F–1(p) = 1,426. По формуле 
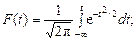
найдем f(t) = 0,1443, по формуле (2.25) определим нормированное смещение у = 26/24×0,1443 = 0,1563.
Из формулы (2.24) следует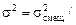 
(1 – ty –y2) = 0,03577/(1 – 1,426×0,1563 – 0,15632) = 0,04752; s = 0,218.
Из формулы (2.23) получаем = хсмещ + sу = 0,451 + 0,218×0,1563 = 0,485. Полученные оценки приведены в табл.2.7.
Таблица 2.7