Выборочная ковариация и выборочная дисперсия

Выборочная ковариация является мерой взаимосвязи между двумя переменными. Данное понятие будет проиллюстрировано на простом примере.

Со времен нефтяного кризиса 1973 г. реальная цена на бензин, т. е. цена бензина, отнесенная к уровню общей инфляции, значительно возросла, и это оказало заметное воздействие на потребительский спрос.

Таблица 1.2

Потребительские расходы на бензин и его реальная цена в США

Год Расходы (млрд. долл., цены 1972 г.) Индекс реальных цен (1972=100)
26,2 103,5
24,8 127,0
25,6 126,0
26,8 124,8
27,7 124,7
28,3 121,6
27,4 149,7
25,1 188,8
25,2 193,6
25,6 173,9

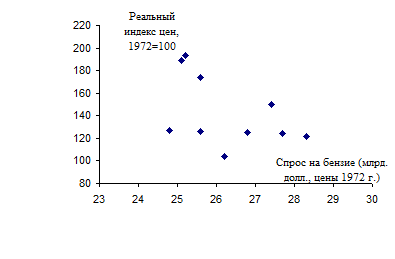
Рис. 1.2. Спрос на бензин в США, 1973 - 1982 гг.

На рис. 1.2 эти данные показаны в виде диаграммы рассеяния. Можно видеть некоторую отрицательную связь между потребительским спросом на бензин и его реальной ценой.

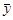Показатель выборочной ковариации позволяет выразить данную связь единым числом. Для его вычисления мы сначала находим средние (для рассматриваемого выборочного периода) значения цены и спроса на бензин. Обозначив цену через p спрос – через y, мы, таким образом, определяем и , которые для этой выборки оказываются равными соответственно 143,36 и 26,27. Затем для каждого года вычисляем отклонение величин p и у от средних и перемножаем их. Для первого года 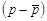равно (103,5 – 143,36), или –39,86, и равно (26,2 – 26,27), или –0,07, а произведение 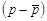составит 2,79. Проделаем это для всех годов выборки и возьмем среднюю величину, она и будет выборочной ковариацией (как видно, не очень сложно вычисляемой).

При наличии п наблюдений двух переменных (х и у) выборочная ковариация между х и у задается формулой:

Для различения ковариационной генеральной и выборочной совокупности используем обозначение с прописной буквы применительно к выборочной ковариации 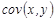и или 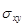для ковариации между х и у в генеральной совокупности.

Аналогичные обозначения используются для дисперсии –применительно к выборочной дисперсии и – к дисперсии для генеральной совокупности.

В примере с бензином детали проведенных вычислений для всей выборки приведены в табл. 1.3. Здесь в столбцах 2 и 3 представлены исходные данные для и 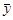. В результирующих строках вычисляются р и у. В столбцах 4 и 5 рассчитываются 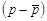и для каждого года, а в столбце эти две величины перемножаются. В нижней клетке последнего столбца определяется средняя величина (–16,24), она и является значением выборочной ковариации.


Таблица 1.3

Наблюдение p y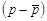
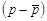
103,5 26,2 -39,86 -0,07 2,79
24,8 -16,36 -1,47 24,05
25,6 -17,36 -0,67 11,63
124,8 26,8 -18,56 0,53 -9,84
124,7 27,7 -18,66 1,43 -26,68
121,6 28,3 -21,76 2,03 -44,17
149,7 27,4 6,34 1,13 7,16
188,8 25,1 45,44 -1,17 -53,16
193,6 25,2 50,24 -1,07 -53,76
173,9 25,6 30,54 -0,67 -20,46
Сумма 1433,6 262,7     -162,44
Среднее 143,36 26,27     -16,24

 

А
D
С
В
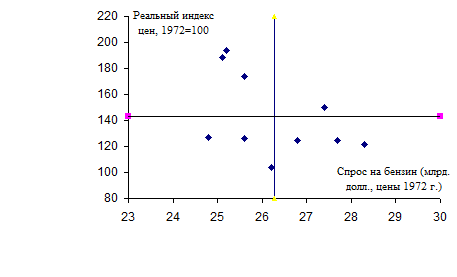Рис. 1.3.

 

Ковариация в данном случае отрицательна. Так это и должно быть. Отрицательная связь, как это имеет место в данном примере, выражается отрицательной ковариацией, а положительная связь – положительной ковариацией.

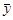Имеет смысл рассмотреть причину этого. Рисунок 1.3 точно такой же, как и рис. 1.2, но здесь диаграмма рассеяния наблюдений делится на четыре части вертикальной и горизонтальной линиями, проведенными через и соответственно. Пересечение этих линий; образует точку 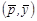, которая показывает среднюю цену и средний спрос за период времени, соответствующий нашей выборке. Используя аналогию из физики, можно сказать, что эта точка является центром тяжести совокупности точек, представляющих наблюдения.

Для любого наблюдения, лежащего в квадранте А, значения реальной цены и спроса выше соответствующих средних значений. Для данных наблюдений как 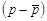, так и являются положительными, а поэтому должно быть положительным и 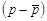. Наблюдение, таким образом, дает положительный вклад в ковариацию. Так, например, наблюдение за 1979г. лежит в этом квадранте и 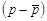=6,34, и =1,13, а их произведение равно 7,16. Далее рассмотрим квадрант В. Здесь наблюдения имеют реальную цену ниже средней и спрос выше среднего. Поэтому 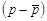отрицательно, положительно, произведение 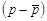отрицательно, и наблюдение вносит отрицательный вклад в ковариацию. Например, наблюдение за 1978 г. Имеет 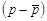=–21,76, =2,03 и 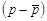, таким образом, равно –44,17.

В квадранте С как реальная цена, так и спрос ниже своих средних значений. Таким образом, 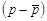и обаявляются отрицательным, а 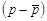положительно. (В качестве примера см. наблюдение за 1974 г.)

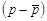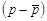
Наконец, в квадранте D реальная цена выше средней, а спрос ниже среднего. Таким образом, положительно, отрицательно, поэтому отрицательно, и в ковариацию, соответственно, вносится отрицательный вклад. (В качестве примера см. наблюдение за 1981 г.)

Поскольку выборочная ковариация является средней величиной произведения 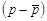для 20 наблюдений, она будет положительной, если положительные вклады будут доминировать над отрицательными, и отрицательной, если будут доминировать отрицательные вклады. Положительные вклады исходят из квадрантов А и С, и ковариация будет, скорее всего, положительной, если основной разброс пойдет по наклонной вверх. Точно так же отрицательные вклады исходят из квадрантов В и D. Поэтому если основное рассеяние идет по наклонной вниз, как в данном примере, то ковариация будет, скорее всего, отрицательной.

Правило 1

Если 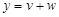, то .

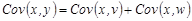Правило2

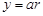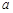Если , где – константа, то .

Правило 3

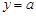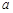Если , где – константа, то .

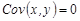Если х и у – случайные величины, то теоретическая ковариация определяется как математическое ожидание произведения отклонений этих величин от их средних значений:

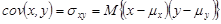(1.12)

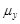где и –теоретические средние значения х и у соответственно.

Как вы и ожидаете, если теоретическая ковариация неизвестна, то для ее оценки может быть использована выборочная ковариация, вычисленная по ряду наблюдений. К сожалению, оценка будет иметь отрицательное смещение, так как

(1.13)

Причина заключается в том, что выборочные отклонения измеряются по отношению к выборочным средним значениям величин х и у и имеют тенденцию к занижению отклонений от истинных средних значений. Очевидно, мы можем рассчитать несмещенную оценку путем умножения выборочной оценки на .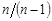

Если х и у независимы, то их теоретическая ковариация равна нулю, поскольку 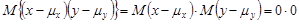благодаря свойству и факту, что М(х) и М(у) равняются соответственно и .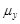

До сих пор термин "дисперсия" использовался в смысле теоретической дисперсии (т.е. относящейся ко всей генеральной совокупности). Для целей, которые прояснятся при обсуждений регрессионного анализа, целесообразно ввести понятие выборочной дисперсии, Для выборки из n наблюдений
(х1, х2, ... , хn) выборочная дисперсия определяется как среднеквадратичное отклонение в выборке:

(1.14)

Сделаем следующие замечания:

1. Определенная таким образом выборочная дисперсия представляет собой смещенную оценку теоретической дисперсии, что s2, определенная как

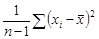
является несмещенной оценкой 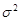. Отсюда следует, что ожидаемое значение величины равно и что, следовательно, она; имеет отрицательное смещение. Отметим, что если размер выборки п становится большим, то 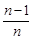стремится к единице и, таким образом, математическое ожидание величины стремится к 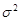. Можно легко показать, что ее предел по вероятности (plim) равен 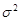и, следовательно, она является примером состоятельной оценки, которая смещена для небольших выборок.

2. Так как величина s2 является несмещенной, то в некоторых работах ее часто определяют как выборочную дисперсию и либо избегают ссылок на , либо дают ей какое-то другое название.

Почему выборочная дисперсия в среднем занижает значение теоретической дисперсии? Причина заключается в том, что она вычисляется как среднеквадратичное отклонение от выборочного среднего, а не от истинного значения. Так как выборочное среднее автоматически находится в центре выборки, то отклонения от него в среднем меньше отклонений от теоретического среднего значения.

Подводя итог вышеизложенному, повторим, что выборочная ковариация

и выборочная дисперсия

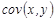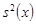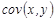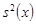смещенные оценки теоретической ковариации и дисперсии , соответственно. Они имеют отрицательное смещение –то есть в большинстве случаев дают значения оценок, меньшие теоретических величин и , соответственно. Несмещенной оценкой теоретической ковариации является оценка , несмещенной оценкойдисперсии – оценка .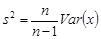

Существует несколько простых и очень полезных правил для расчета дисперсии, являющихся аналогами правил для ковариации. Эти правила в равной степени можно использовать как для выборочной, так и для теоретической дисперсии.

Правило дисперсии 1

Если 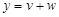, то .

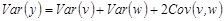Правило дисперсии 2

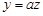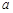Если , где – константа, то .

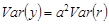Правило дисперсии 3

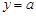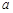Если , где – константа, то .

Правило дисперсии 4

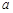Если , где – константа, то .

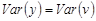Во-первых, заметим, что дисперсия переменной х может рассматриваться как ковариация между двумя величинами х:

(1.15)

Учитывая это равенство, мы можем воспользоваться правилами расчета выборочной ковариации, чтобы вывести правила расчета дисперсии. Кроме того,

(1.16)

Ковариация весьма удобна с математической точки зрения, что является особенно хорошим измерителем взаимосвязи между величинами. Более точной мерой зависимости является тесно связанный с ней коэффициент корреляции.

Подобно дисперсии и ковариации, коэффициент корреляции имеет две формы – теоретическую и выборочную. Теоретический коэффициент корреляции традиционно обозначается греческой буквой . Для переменных х и у этот коэффициент определяется следующим образом:

. (1.17)

Если х и у независимы, то равно нулю, так как равна нулю теоретическая ковариация. Если между переменными существует положительная зависимость, то , а следовательно, и , будут положительными. Если существует строгая положительная линейная зависимость, то примет максимальное значение, равное 1. Аналогичным образом при отрицательной зависимости будет отрицательным с минимальным значением –1.

Выборочный коэффициент корреляции определяется путем замены теоретических дисперсий и ковариации в выражении (1.17) на их несмещенные оценки. Мы показали, что такие оценки могут быть получены умножением выборочных дисперсий и ковариации на 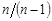. Следовательно,

. (1.18)

Множители 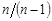сокращаются, поэтому можно определить выборочную корреляцию как

. (1.19)

Подобно величине , имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у (когда на диаграмме рассеяния все точки находятся точно на восходящей прямой линии). Аналогичным образом принимает минимальное значение –1, когда существует линейная отрицательная зависимость (точки лежат точно на нисходящей прямой линии). Величина показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Разумеется, тот факт, что , необязательно означает, что и наоборот.

Выборочная корреляция – несмещенная оценка теоретической корреляции .