Точечная оценка погрешности среднего значения

Среднее значение из n независимых значений случайной величины х также является случайной величиной. Если случайная величина х имеет дисперсию s², то среднее значение , имеет дисперсию d² в n раз меньше:

d² = s²/n или 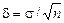. (2.20)

Величину d можно рассматривать как абсолютную среднеквадратичную случайную погрешность среднего значения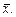

Если разделить обе части равенства (2.20) на среднее значение 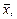то получим относительную погрешность

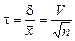, (2.21)

где V – коэффициент вариации. Относительная погрешность может быть выражена в долях единицы или в процентах.

Формулы (2.20) и (2.21) показывают, что погрешность среднего значения прямо пропорциональна изменчивости случайной величины и обратно пропорциональна корню квадратному из числа измерений.

Это позволяет решать две задачи: 1) оценивать абсолютную d или относительную t погрешность среднего значения при известном числе наблюдений n; 2) находить необходимое число измерений n для достижения заданной погрешности среднего значения.

Пример 2. В результате анализа 16 проб гранита рассчитано среднее содержание кремнезема = 70,35 % и среднеквадратичное отклонение s² = 3,20 %. Определить, чему равна среднеквадратичная погрешность среднего содержания и сколько дополнительно нужно взять проб, чтобы снизить относительную погрешность до 1 %.

Решение: Абсолютная среднеквадратичная случайная погрешность d = 3,20/= 0,80 %; относительная случайная погрешность t = 0,80/70,35 = 1,14 %.

Продолжим задачу. Если t = 1 % = 0,01, то из формулы (2.21) получим 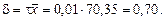Из формулы (2.20) имеем n = s²/d² = 3,20²/0,70² = 21. Следовательно, дополнительно нужно взять и проанализировать 21 – 16 = 5 проб.