Пересечение прямой с поверхностью или плоскостью

(основная задача НГ)

Подобные задачи решаются с помощью посредников.

Задача1

Дано: ∑ - пов-ть (или пл-ть), в данном случае эллипсоид;

 

ℓ- прямая.

 

Рис.42.

Построить точки пересечения ∑ и ℓ.

Алгоритм решения задачи:

1. Через прямую ℓ проводим вспомогательную плоскость – посредник Г. ℓ Î Г

2. Строится ЛП вспомогательной пл-ти Г с заданной пов-тью ∑:

Г ∩ ∑ Þ m (ЛП)

3. Находятся точки пересечения А и В заданной прямой ℓ с построенной ЛП m:

ℓ ∩ m Þ А и В – точки пересечения.

4. Определяется видимость прямой ℓ.

 

Задача 1. Построить т-ку пересечения прямой ℓ с пл-тью общего положения, заданного ∆ АВС (рис.50.) (основная позиционная задача)

Решение:

 

Алгоритм решения задачи:

1). Выбор посредника

Q ^ π₂ Þ Qπ₂ Î ℓ

2). Построение ЛП Q с заданной пл-тью ∆ АВС

Q ∩ ∑ Þ (1₂ – 2₂) Þ (1₁ – 2₁) – ЛП

3). Опред. точки пересечения прямой с пл-тью

ℓ ∩ (1 - 2) Þ т. В

4). Опред. видимость прямой ℓ методом конкурирующих т-ек.

 

Рис.43.

Задача2. Построить точки пересечения прямой n с пов-тью сферы.

Решение:

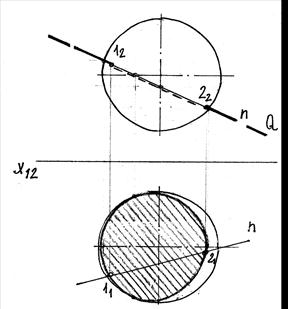
Рис.44.

 

Лекция 8