Общий случай пересечения поверхностей

Общий случай пересечения поверхностей – происходит тогда, когда обе пересекающиеся поверхности занимают общее положение в пространстве относительно плоскостей пр-ий. Задачи решаются с помощью посредников. Посредники выбираются так, чтобы линии пересечения с данными поверхностями были наиболее простыми и просто строились на чертеже. К таким линиям относятся прямые и окружности.

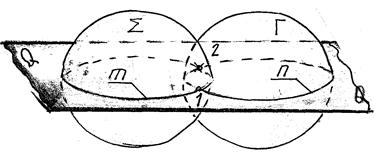
Предположим, пов-ть ∑ пересек-ся с пов-тью Г. В качестве посредника выбираем пл-ть горизонтального уровня Q.

∑ ∩ Г Þ ℓ -?

Плоскость Q пересекает обе пов-ти по кривым линиям m и n. Эти линии, пересекаясь между собой, дают точки 1 и 2, принадлежащие Рис.40. одновременно 3 пов-ям,

а следовательно, и линии пресечения данных пов-тей ∑ и Г.

Определив указанным приёмом необходимое количество т-ек и соединив их в определённой последовательности с учётом видимости, получим искомую линию пересечения (ЛП) пов-тей.

На лп двух пов-тей определяют экстремальные точки (наинизшая и наивысшая), а также точки перехода видимости.

 

Алгоритм решения:

1. Выбор посредника Q.

2. ∑ ∩ Q Þ m (ЛП).

Г ∩ Q Þ n (ЛП).

m и n Î разным поверхностям, но лежат в общей пл-ти Q.

3. m ∩ n Þ точка1 и точка 2 (общие точки).

4. Определение видимости ЛП и поверхностей.

 

Задача1. Построить ЛП 2-х пл-тей общего положения ∑ и Г.

Поверхности ∑ и Г ∩ Q.