Выборка и генеральная совокупность

Фундаментальными понятиями статистического анализа являются понятия вероятности и случайной величины (переменной). Случайной переменной мы называем переменную, которая под воздействием случайных факторов может с определенными вероятностями принимать те или иные значения из некоторого множества чисел. Это переменная, которой (даже при фиксированных обстоятельствах) мы не можем приписать определенное значение, но можем приписать несколько значений, которые она принимает с определенными вероятностями. Под вероятностью некоторого события (например, события, состоящего в том, что случайная переменная приняла определенное значение) обычно понимается доля числа исходов, благоприятствующих данному событию, в общем числе возможных равновероятных исходов. Категория "равновероятные исходы" не определяется, а принимается интуитивно. Например, при "бросании монеты" выпадение орла и решки считается равновероятным (вероятность каждого равна 1/2), а случайная величина числа "орлов" при одном "бросании монеты" может быть равна 0 или 1 с вероятностями 1/2.

Совокупность значений {хк} случайной величины х вероятностей {Рк}, с которыми она их принимает, называют законом распределения случайной величины. Функция Р{х}, как и любая функциональная зависимость, может быть представлена в форме таблицы, формулы или графика. Например, закон распределения числа очков при бросании игрального кубика может быть представлен в виде таблицы:

 

X
р	1/6	1/6	1/6	1/6	1/6	1/6

 

Очевидно, что сумма всех этих вероятностей должна равняться единице, поскольку считаем, что с вероятностью "единица" переменная принимает хоть какое-нибудь из этих значений. Обычная (неслучайная, или детерминированная) переменная является предельным случаем случайной переменной, принимая единственное (при фиксированных обстоятельствах) значение с вероятностью "единица".

Различают дискретные и непрерывные случайные величины. Случайная величина дискретна, если результаты наблюдений представляют собой конечный или счетный набор возможных чисел. Случайная величина непрерывна, если ее значения могут лежать в некотором континууме возможных значений. (Это предполагает, что их нельзя пересчитать, ставя в соответствие им натуральные числа 1,2,....). Значения непрерывной случайной величины могут лежать на отрезке, интервале, луче и т. д.

В основе математической статистики лежат понятия генеральной совокупности и выборки (выборочной совокупности).

Под генеральной совокупностью мы подразумеваем все возможные наблюдения интересующего нас показателя, все исходы случайного испытания или всю совокупность реализаций случайной величины х. Пример генеральной совокупности – данные о доходах всех жителей какой-либо страны, о результатах голосования населения по какому-либо вопросу и т.д. Однако в большинстве случаев мы имеем дело только с частью возможных наблюдений, взятых из генеральной совокупности, и называем это множество (точнее подмножество) значений выборкой. Таким образом, выборка – это множество наблюдений, составляющих лишь часть генеральной совокупности. Выборка объема n – это результат наблюдения случайной величины в вероятностном эксперименте, который повторяется n раз в одних и тех же условиях (которые могут контролироваться), а, следовательно, и при неизменном распределении случайной величины х. Процесс, который приводит к получению выборочных данных, называют выборочным исследованием.

Мы обычно говорим о генеральной совокупности, когда используем определенные теоретические модели, но на практике в нашем распоряжении имеются лишь выборочные данные, и поэтому мы можем строить оценки теоретических характеристик, основываясь лишь на данных выборочных наблюдений. Мы обсудим соотношение между теоретическими характеристиками и их выборочными оценками позднее. Подчеркнем лишь, что целью математической статистики является получение выводов о параметрах, виде распределения и других свойствах случайных величин (генеральной совокупности) по конечной совокупности наблюдений – выборке.

Выборку называют репрезентативной (представительной), если она достаточно полно представляет изучаемые признаки и параметры генеральной совокупности. Для репрезентативности выборки важно обеспечить случайность отбора, с тем, чтобы все объекты генеральной совокупности имели равные вероятности попасть в выборку. Для обеспечения репрезентативности выборки применяют следующие способы отбора: простой отбор (последовательно отбирается первый случайно попавшийся объект), типический отбор (объекты отбираются пропорционально представительству различных типов объектов в генеральной совокупности), случайный отбор – например, с помощью таблицы случайных чисел и т.п.

Итак, выборка– некоторое количество наблюдений, отобранных из генеральной совокупности, а наблюдение– наблюдаемое значение случайной величины или набора случайных величин.

В эконометрике всегда известна только выборка из некоторого количества наблюдений случайной величины, и по данным выборки можно рассчитать только выборочные, а не теоретические характеристики этой случайной величины.

1.1.5. Выборочные и теоретические величины.
Оценки как случайные величины. Оценки х и S²

Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений, причем в качестве весового коэффициента берется вероятность соответствующего исхода. Вы можете рассчитать его, перемножив все возможные значения случайной величины на их вероятности и просуммировав полученные произведения. Математически, если случайная величина обозначена как х, то ее математическое ожидание обозначается как М(х).

Предположим, что х может принимать n конкретных значений (х₁, х₂, ... , х_n) ичто вероятность получения х_j равна р_i Тогда

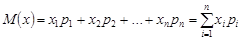(1.1)

Рассмотрим простой пример случайной переменной – число очков, выпадающее при бросании лишь одной игральной кости.

В данном случае возможны шесть исходов: n₁ = 1, х₁ = 2, х₂ = 3, х₃ = 4,
х₄ = 5, х₅ = 6. Каждый исход имеет вероятность 1/6, поэтому здесь

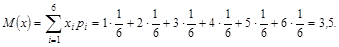(1.2)

В данном случае математическим ожиданием случайной переменной является число, которое само по себе не может быть получено при бросании кости.

Математическое ожидание случайной величины часто называют ее средним по генеральной совокупности. Для случайной величины х это значение часто обозначается как .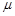

Важной функцией переменной х является ее теоретическая дисперсия, которая характеризует меру разброса для вероятного распределения. Она определяется как математическое ожидание квадрата разности между величиной х и ее средним, т.е. величины 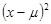, где 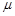–математическое ожидание х. Дисперсия обычно обозначается как 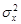, и если ясно, о какой переменной идет речь, то нижний индекс может быть опущен.

Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайную составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если х – случайная переменная и 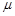– ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом:

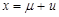(1.3)

где и – чисто случайная составляющая (в регрессионном анализе она обычно представлена случайным членом).

Случайная составляющая и определяется как разность между х и :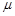

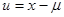(1.4)

Из определения следует, что математическое ожидание величины и равно нулю. Из уравнения (1.4) имеем:

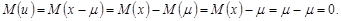(1.5)

Поскольку весь разброс значений х обусловлен и, неудивительно, что теоретическая дисперсия х равна теоретической дисперсии и. Последнее нетрудно доказать. По определению,

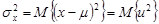(1.6)

Таким образом, 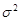может быть эквивалентно определена как дисперсия х или и.

Обобщая, можно утверждать, что если х – случайная переменная, определенная по формуле (1.3), где 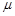– заданное число, и – случайный член с М(и)=0 и дисперсией D(u), то математическое ожидание величины х равно 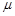, а дисперсия – .

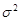До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности – об ее распределении вероятностей (в случае дискретной переменной) или о функции плотности распределения (в случае непрерывной переменной). С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики, в которых мы можем быть заинтересованы.

Однако на практике, за исключением искусственно простых случайных величин (таких, как число выпавших очков при бросании игральной кости), мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.

Процедура оценивания всегда одинакова. Берется выборка из п наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Нужно следить за терминами, делая важное различие между способом или формулой оценивания и рассчитанным по ней для данной выборки числом, являющимся значением оценки.

Оценка, способ оценивания (estimator)– общее правило, формула для получения приближенного численного значения какого-либо параметра по данным выборки, а значение оценки (estimation)– число, полученное в результате применения оценки к конкретной выборке; является случайной величиной, значение которой зависит от выборки.

В табл. 1.1 приведены формулы оценивания для двух важнейших характеристик генеральной совокупности. Выборочное среднее х обычно дает оценку для математического ожидания, а формула s² в табл. 1.1 – оценку дисперсии генеральной совокупности.

Таблица 1.1

Характеристики генеральной совокупности	Формулы оценивания
Среднее,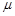
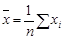
Дисперсия, s2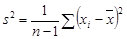

 

Отметим, что это обычные формулы оценки математического ожидания и дисперсии генеральной совокупности, однако не единственные. Конечно, не все формулы оценки, которые можно представить, одинаково хороши. Причина, по которой в действительности используется х, в том, что эта оценка в наилучшей степени соответствует двум очень важным критериям – несмещенности и эффективности. Эти критерии будут рассмотрены ниже.

Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х – случайная переменная u, следовательно, случайной величиной является и функция набора ее значений. Возьмем, например, 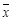– оценку математического ожидания:

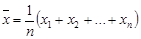(1.7)

Мы только что показали, что величина х в i-м наблюдении может быть разложена на две составляющие: постоянную часть 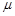и чисто случайную составляющую и_i

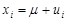(1.8)

Следовательно,

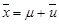(1.9)

где 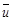– выборочное среднее величин и_i

Отсюда можно видеть, что 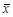, подобно х, имеет как фиксированную, так и чисто случайную составляющие. Ее фиксированная составляющая 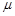, то есть математическое ожидание х, а ее случайная составляющая 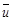, то есть среднее значение чисто случайной составляющей в выборке.

Функции плотности вероятности для х и 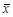показаны на одинаковых графиках (рис. 1.1). Как показано на рисунке, величина х считается нормально распределенной. Можно видеть, что распределения, как х, так и 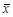, симметричны относительно 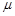– теоретического среднего. Разница между ними в том, что распределение 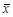уже и выше. Величина 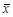, вероятно, должна быть ближе к 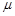, чем значение единичного наблюдения х, поскольку ее случайная составляющая 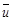есть среднее от чисто случайных составляющих 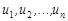в выборке, которые, по-видимому, "гасят" друг друга при расчете среднего. Далее, теоретическая дисперсия величины 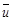составляет лишь часть теоретической дисперсии и.

 

Рис. 1.1. Сравнение функций плотности вероятности одиночного наблюдения и выборочного среднего

 

Величина s² – оценка теоретической дисперсии х – также является случайной переменной. Вычитая (1.9) из (1.8), имеем:

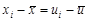(1.10)

Следовательно,

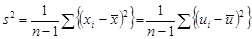(1.11)

Таким образом, s² зависит от (и только от) чисто случайной составляющей наблюдений х в выборке. Поскольку эти составляющие меняются от выборки к выборке, также от выборки к выборке меняется и величина оценки s².