Линейчатые поверхности

Линейчатые поверхности образуются непрерывным движением прямой по некоторой направляющей (прямая, ломаная или кривая линия).

Рассмотрим поверхности, образованные движением образующей, один конец которой проходит через неподвижную т-ку S, а второй - перемещается по направляющей m.

Определительтакой поверхности имеет вид: Σ (S, m),

где S – конечная точка, m – направляющая.

Поверхности, образующиеся в данной группе:

а) коническая поверхность, где направляющая – кривая, образуется движением прямолинейной образующей ℓ, скользящей по ней m и проходящей во всех своих положениях через одну фиксированную т-ку S (не лежащую на криволинейной направляющей), называемую вершиной конической поверхности.

 

S – конечная точка

m – кривая линия

 

частный случай: конус, где m - окружность

 

б) пирамидальная поверхность образуется движением прямолинейной образующей ℓ по ломаной направляющей m и проходящей через фиксированную т-ку (вершину) S.

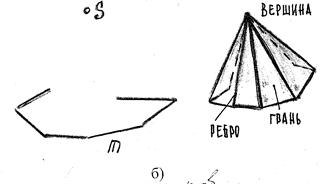
S S – конечная точка;

M m – ломаная линия

 

частный случай: пирамида, где m – правильный многоугольник

 

в) цилиндрическая поверхностьобразуется движением прямой ℓ, имеющей постоянное направление ↑ , S бесконечно удалена, т.е. все образующие двигаются относительно друг-друга параллельно.

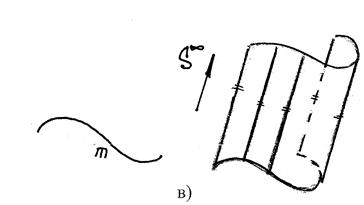S^∞–бескон.удаленная точка

m – кривая линия

 

частный случай: цилиндр,

где m – окружность,

i – ось вращения

г) призматическая поверхность образуется движением прямолинейной образуюей по некоторой ломаной направляющей, при этом S бесконечно удалена.

S^∞ – бесконечно удаленная точка

m – ломаная линия

 

 

Рис.32. частный случай: призма,

где m - ломаная

 

Рассмотрим задачу.

Задача 1. По заданному определителю построить каркас и очерк поверхности. Построить недостающую пр-ию точки А, принадлежащую данной поверхности.

Решение:

Итак, поверхность задана определителем Σ (S, m), S- конечная точка, проекция направляющей – ломаная линия, следовательно, это пирамидальная поверхность.

 

 

Рис.33.