Прямые частного положения

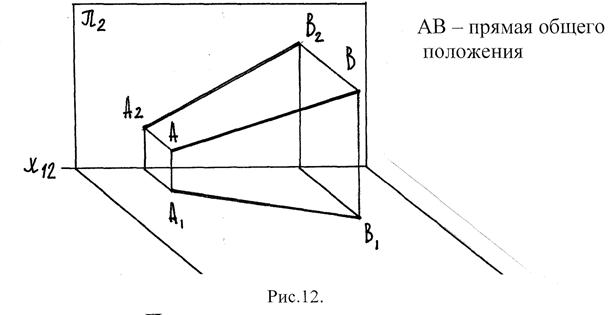
Изображение прямой общего положения на эпюре

Прямые в пространстве могут быть ^, || с плоскостями проекций, занимать общее положение.

Если прямая не || и не ^ ни одной из плоскостей проекций – она наз-ся прямой общего положения.

Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо плоскости проекций. Существуют 6 прямых частного положения, которые, в свою очередь делятся на две группы:

2.3.1 Прямые уровня – это прямые, параллельные какой-либо плоскости пр-ий, их три (рис.13 а-в):

 

f – фронталь h – горизонталь p-профиль. прямая

 

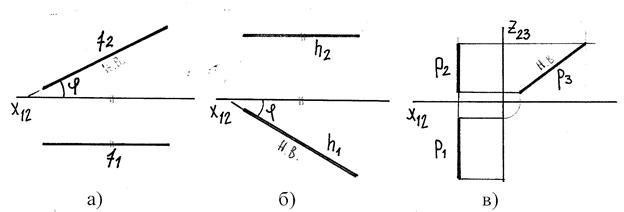
f || П₂ в простр-ве h || П₁ в простр-ве р || П₃ в простр-ве

f₂ – н.в. на черт. h₁ – н.в. на черт. р₃ – н.в. на черт.

f₁ || оси Х₁₂ h ₂ || оси Х₁₂ р₁ и р₂ ^ Х₁₂

φ-угол с пл-тью π₁; φ- угол с пл-тью π₂;

 

2.3.2 Проецирующие прямые – это прямые, перпендикуляр-ные какой-либо плоскости проекций, их три (рис.13 г-е):

 

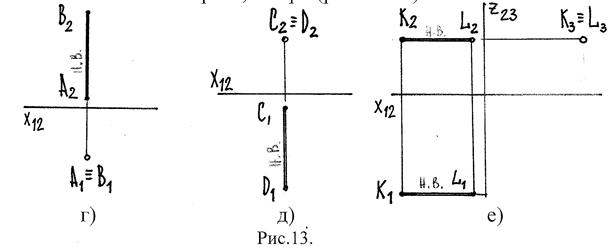
АВ-горизонт.-проецир. СД-фронт.-проецир. KL-профил.-проецир. прямая прямая прямая

АВ^ π₁ в простр-ве СД^π₂ в простр-ве КL^π₃ в простр-ве

А₂В₂^Х₁₂ - н.в.на черт.С₁Д₁^Х₁₂ – н.в. на черт. K₂L₂, K₁L₁ || Х₁₂ н.в.

А₁≡ В₁ – точка С₂ ≡ Д₂ – точка K₃ ≡ L₃ – точка

 

Если в пространстве прямая расположена в плоскости проекций, то на чертеже одна из ее проекций совпадает с осью Х₁₂

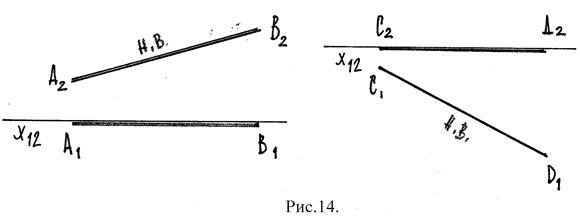
АВ Î П₂ – в пространстве CD Î П₁ – в пространстве

А₁В₁≡Х₁₂ на черт. С₂D₂ ≡ Х₁₂ на черт.

А₂В₂ – н.в. С₁Д₁ – н.в.