Диапазон центровок ЛА
На крылатых ракетах, вертолётах и самолётах выделяют положение “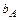 ”- т. е. САХ и положение центра масс (тяжести) ЛА относительно
”- т. е. САХ и положение центра масс (тяжести) ЛА относительно 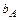 (рис.61)
(рис.61)
|
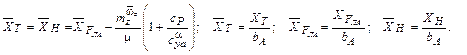 (10.15)
(10.15)
При положении ЦМ (ЦТ) в точке 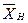 самолёт (ракета) становятся нейтральными. Эта точка находится позади фокуса, т.к.
самолёт (ракета) становятся нейтральными. Эта точка находится позади фокуса, т.к. 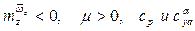 обычно >0. Величина
обычно >0. Величина 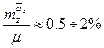 САХ, т.е. различие между
САХ, т.е. различие между 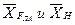 невелик.
невелик.
Предельно заднее положение ЦТ определяется как
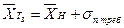 ; (10.16)
; (10.16)
где: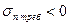 - требуемый запас статической устойчивости по принятым нормативам.
- требуемый запас статической устойчивости по принятым нормативам.
Предельно переднее положение ЦТ определяется по условиям балансировки ЛА обычно в прямолинейном полёте, т.е. при 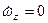
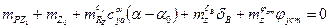 . (10.17)
. (10.17)
Здесь: 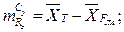
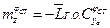
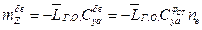 ;
;
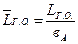 -относительное плечо горизонтального оперения (рис.62).
-относительное плечо горизонтального оперения (рис.62).
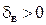



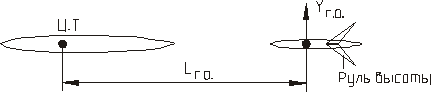
Рис. 62
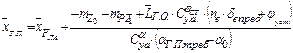 , (10.18)
, (10.18)
где 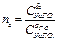 -коэффициент относительной эффективности руля высоты;
-коэффициент относительной эффективности руля высоты;
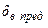 - предельное положение руля высоты;
- предельное положение руля высоты;
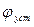 - угол установки стабилизатора;
- угол установки стабилизатора;
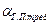 - требуемый угол атаки для горизонтального полёта;
- требуемый угол атаки для горизонтального полёта;
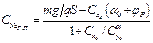 ;
; 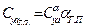
(см. ”метод тяг”), откуда получаем
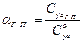 ; (10.19)
; (10.19)
Предельно передняя центровка 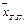 определяется для наихудших условий обычно при заходе на посадку с учётом выпущенных закрылков, щитков и другой механизации. Эксплуатационная область допустимых центровок выбирается, как показано на рис. 61, с учётом всего диапазона скоростей полёта.
определяется для наихудших условий обычно при заходе на посадку с учётом выпущенных закрылков, щитков и другой механизации. Эксплуатационная область допустимых центровок выбирается, как показано на рис. 61, с учётом всего диапазона скоростей полёта.
Нетрудно видеть, что с ростом относительной площади 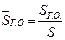 и плеча
и плеча 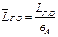 горизонтального оперения т.е. статического момента оперения AГ.О.
горизонтального оперения т.е. статического момента оперения AГ.О. 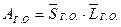 фокус ЛА, а значит
фокус ЛА, а значит 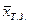 сдвигается назад. Одновременно, при неизменной относительной площади руля высоты
сдвигается назад. Одновременно, при неизменной относительной площади руля высоты 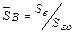 растёт эффективность орга- нов управления и
растёт эффективность орга- нов управления и 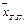 сдвигается вперед (см.рис.63).
сдвигается вперед (см.рис.63).
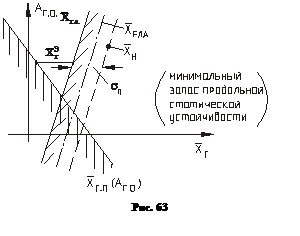
Из условия 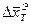 потребного можно найти значение АГ.О. и все параметры горизонтального оперения. Аналогично решаются все задачи по выбору вертикального оперения.
потребного можно найти значение АГ.О. и все параметры горизонтального оперения. Аналогично решаются все задачи по выбору вертикального оперения.
11.Исследование возмущённого движения ЛА
11.1 Уравнения возмущённого движения ЛА
Собирая вместе динамические и кинематические уравнения движения ЛА, как материальной точки, и его вращательного движения вокруг центра масс, обозначим их в виде системы нелинейных дифференциальных уравнений:
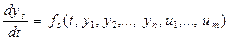 ;
; 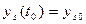 , (s=1,2,…n) (11.1)
, (s=1,2,…n) (11.1)
Здесь y1,…,yn – фазовые переменные, u1,…,un – управляющие воздействия на ЛА, fs(…)-нелинейные функции. Фазовыми переменными являются: 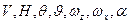 ,… и т.д. Управляющие воздействия:
,… и т.д. Управляющие воздействия: 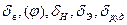 , Р,… и т.д. t – независимая переменная; чаще всего – время.
, Р,… и т.д. t – независимая переменная; чаще всего – время. 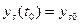 - начальные условия при t=t0.
- начальные условия при t=t0.
Пусть для заданных 
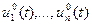 существует опорная (программная, невозмущенная) траектория движения ЛА (рис. 64).
существует опорная (программная, невозмущенная) траектория движения ЛА (рис. 64).

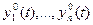 , удовлетворяющие (11.1)
, удовлетворяющие (11.1)
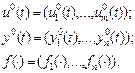
Полагаем, что при движении ЛА действуют возмущения: 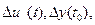 ветер и др., которые приводят к отклонению движения от опорной (программной, невозмущенной) траектории, а суммарное движение описывается вектор-функциями
ветер и др., которые приводят к отклонению движения от опорной (программной, невозмущенной) траектории, а суммарное движение описывается вектор-функциями
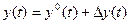 ,
, 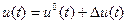
и в соответствии с (11.1) (в векторной форме)
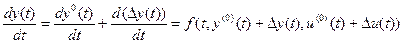 . (11.2)
. (11.2)
Опорная траектория описывается уравнением
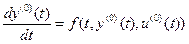 ;
; 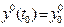 (11.3)
(11.3)
Раскладывая правую часть (11.2) в ряд Тейлора относительно опорных значений y0(t), u0(t), ограничиваясь линейными членами и вычитая (11.3) из (11.2), получаем
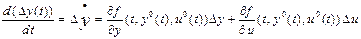 . (11.4)
. (11.4)
Здесь мы воспользовались “методом малых возмущений” в соответствии с которым составляющие более высокого порядка по сравнению с линейными становятся пренебрежимо малыми.
Систему линейных дифференциальных уравнений (11.4) можно разделить на простые подсистемы, которые можно исследовать независимо друг от друга. Например, если в уравнениях (5.2),(5.3) обозначить 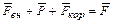 ,
, 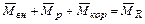 и их проекции соответственно на траекторные и связанные оси координат обозначить как:
и их проекции соответственно на траекторные и связанные оси координат обозначить как:
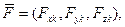
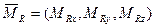 , то разделить уравнения в случае опорной траектории – прямолинейного полёта без крена и скольжения можно при следущих допущениях:
, то разделить уравнения в случае опорной траектории – прямолинейного полёта без крена и скольжения можно при следущих допущениях: 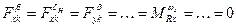 ;
; 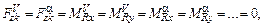
в которых параметрами принимаются (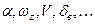 ) – для описания продольного возмущенного движения, (
) – для описания продольного возмущенного движения, (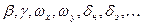 ) – для описания бокового движения.
) – для описания бокового движения.
Система уравнений, описывающих продольное возмущённое движение (в отклонениях от опорного)
1. 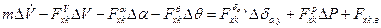 ;
;
2. 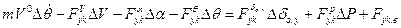 ;
;
3. 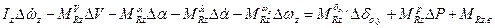 ;
;
4. 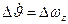 ; (11.5)
; (11.5)
5. 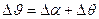 ;
;
6. 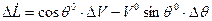 ;
;
7. 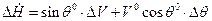 ;
;
Система уравнений бокового возмущённого движения (в отклонениях от опорного)
1. -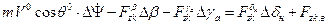 ;
;
2. 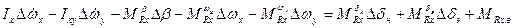 ;
;
3. 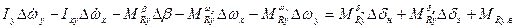 ;
;
4. 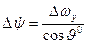 ;
;
5. 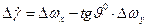 ; (11.6)
; (11.6)
6. 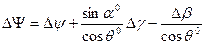 ;
;
7.  ;
;
8. 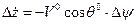 .
.
В уравнениях (11.5), (11.6) величины Fxk.в; Fyk.в; Fzk.в; MRx.в; MRy.в; MRz.в представляют собой возмущающие силы и моменты, не обусловленные непосредственно изменениями кинематических параметров. Это обычно функции параметров атмосферы, либо другие известные функции. Система (11.5) может быть разделена на две подсистемы, описывающие короткопериодическое (уравнения 2, 3, 4, 5) и длиннопериодические движения Л.А. (1, 6, 7).
 Рассмотрим подробнее математическую модель, описывающую короткопериодическое движение. Используя стандартные матричные обозначения для уравнений собственного возмущенного движения ( ∆u(t)≡0 ) ∆
Рассмотрим подробнее математическую модель, описывающую короткопериодическое движение. Используя стандартные матричные обозначения для уравнений собственного возмущенного движения ( ∆u(t)≡0 ) ∆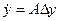 ; A=[aij], из (2),(3),(4),(5) получаем
; A=[aij], из (2),(3),(4),(5) получаем
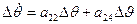 ;
;
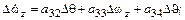
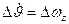 ;
; 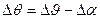 ;
; 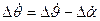 ,
,
где: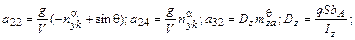
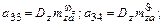
Если принять за исходный опорный режим полета – горизонтальный и положить 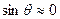 , то часть системы преобразуется к виду:
, то часть системы преобразуется к виду:
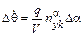 ;
;
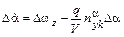 .
.
Уравнение для 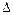
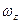 представим в несколько другой форме, используя третье уравнение системы (11.5)
представим в несколько другой форме, используя третье уравнение системы (11.5)
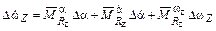 ;
;
где; 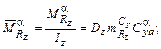
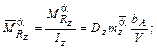
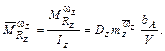 ;
;
Дифференцируя уравнение для 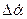 и подставляя последнее, получаем уравнение собственного короткопериодического быстрого вращательного движения ЛА с почти неизменной скоростью.
и подставляя последнее, получаем уравнение собственного короткопериодического быстрого вращательного движения ЛА с почти неизменной скоростью.
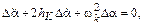
где: 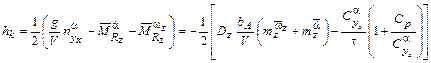 ;
; 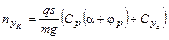 ;
; 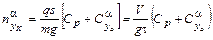 ;
; 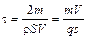 ;
; 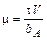 ;
; 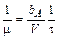 ;
; 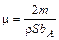 ,
,
а также: 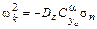 ,
, 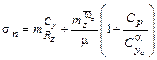 ,
, 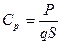 .
.
Аналогично выводятся уравнения для медленной составляющей продольного длиннопериодического движения и ненулевых управляющих воздействий на ЛА 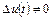 .
.
Лекция 16.
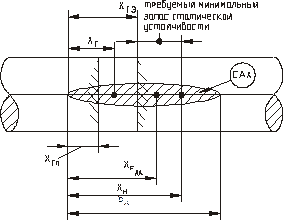 Рис. 61 а)
Рис. 61 а)



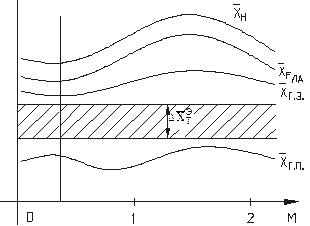 Рис. 61 б)
Рис. 61 б)