Пример 2.
2 листа бумаги сходятся при выдувании воздуха между ними.
Пример 3 (рис.11).
Пульверизатор
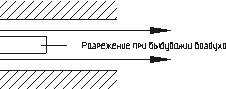
Рис. 11
Распределение давления на профиле можно получить экспериментально, просверлив отверстия в различных точках крыла на нижней и верхней поверхности (дренировав) и поставив датчики давлений. Такие дренированные модели крыльев ЛА продуваются в аэродинамических трубах. Рассмотрим физическую картину возникновения аэродинамических сил на прямоугольном крыле (профиле).
| Примеры (рис. 12-14). | Симметричный профиль | ||||
 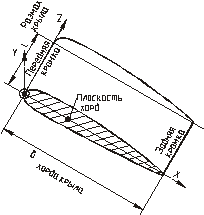 Рис. 12
Рис. 12
|
              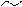 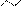 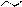 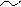  
    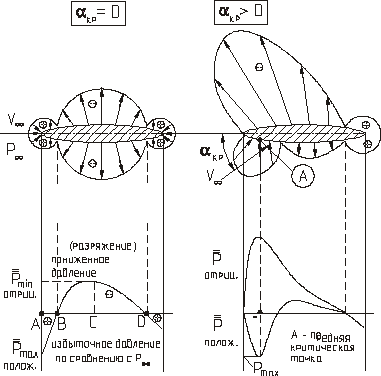
Рис. 13 | ||||
В т. B,D –скорости потока равны 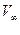 , т.к. , т.к. 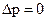 , ,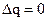 В т. A, V=0, pmax
В т. A, V=0, pmax
|
Координатные диаграммы распределения давления.
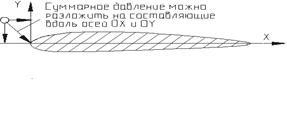
Рис. 14
Рассмотрим профиль и схему элементарных действующих сил на него в связанной с носком профиля системе координат OXY (рис. 15).
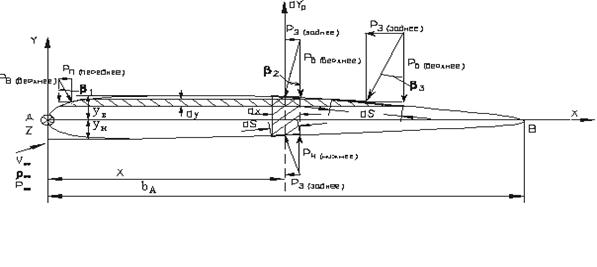
Рис. 15
Для прямоугольного крыла размаха  выделим участки профиля с размерами dx и dy.Учитывая, что
выделим участки профиля с размерами dx и dy.Учитывая, что 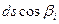 =dx определим элементарную нормальную силу от давления на элемент крыла
=dx определим элементарную нормальную силу от давления на элемент крыла 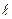 dx
dx
dYp=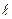 (pн –pв)dx
(pн –pв)dx 
Аналогично для элементарной продольной силы от давления
dXр=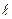 (pп –pз )dy
(pп –pз )dy
Интегрируя эти выражения соответственно от A до B вдоль оси OX и от yн до yв вдоль оси OY,получим формулы для нормальной и продольной сил без учета сил трения
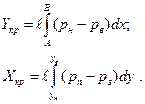
Записав выражение для элементарного момента от нормальной силы (момент от продольной силы обычно пренебрежимо мал, в силу того что крыло обычно “тонкое”) относительно точки A
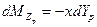
Определим продольный момент крыла от давления
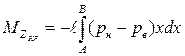
Здесь минус принят в виду того, что момент направлен против часовой стрелки, если смотреть вдоль 0Z, расположив ее от нас вдоль передней кромки.
В этих формулах целесообразно перейти от сил к их коэффициентам, учитывая, что площадь S прямоугольного крыла S = b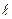 , а также принимая, что (здесь формулы объединены в записи)
, а также принимая, что (здесь формулы объединены в записи)
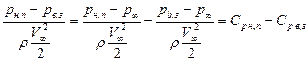
В частности для Y, полагая
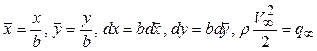 ;
;
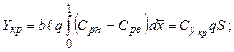 (3.3)
(3.3)
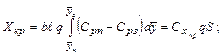 (3.4)
(3.4)
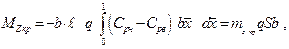 (3.5)
(3.5)
где:
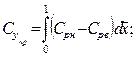
 (3.6)
(3.6)
В формулах (3.3) ¸ (3.5) и в дальнейшем индекс (∞) опущен в выражениях V∞ и q∞, если не оговаривается особо.
 На практике крылья ЛА, как правило, отличаются от прямоугольной формы, поэтому для удобства расчетов и сравнительного анализа крыльев ЛА вводят понятие средней аэродинамической хорды (САХ)(см. рис.16).
На практике крылья ЛА, как правило, отличаются от прямоугольной формы, поэтому для удобства расчетов и сравнительного анализа крыльев ЛА вводят понятие средней аэродинамической хорды (САХ)(см. рис.16).
Для крыла произвольной формы в плане подбирается такое эквивалентное прямоугольное, момент МZ Э которого, силы YЭ, XЭ и площадь SЭ были бы равны исходным MZ.ИСХ, YИСХ, XИСХ,SИСХ.
 MZ Э(xA, yA,bA,
MZ Э(xA, yA,bA,  )= MZ КР ИСХ ;
)= MZ КР ИСХ ;
YЭ(xA,yA,bA,  )= YКР ИСХ ; (3.7)
)= YКР ИСХ ; (3.7)
XЭ(xA,yA,bA, 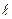 )= XКР ИСХ;
)= XКР ИСХ;
SЭ=bA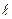 =SИСХ.
=SИСХ.
Из четырех уравнений определяются хA, yA, bA, 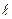 .
.
Здесь xA, yA- координаты эквивалентного прямоугольного крыла в системе осей OXY, связанной с носком исходного крыла; bA- значение САХ; 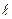 - размах эквивалентного крыла. Остальные параметры профиля эквивалентного крыла можно оставить прежними и равными исходным.
- размах эквивалентного крыла. Остальные параметры профиля эквивалентного крыла можно оставить прежними и равными исходным.
Лекция 3.