Аэродинамические силы и продольный момент изолированного крыла

Характеристики Земли, ее атмосферы (см. рис.1)

 

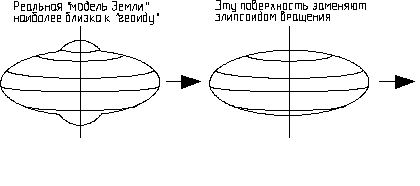
Более грубая модель Земли – сфера с Rз=6371 км и вектором угловой скорости суточного вращения .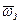

Наиболее простая модель Земли – местная горизонтальная плоскость (М.Г.П.).

Рис. 1

Эллипсоид вращения, сфера используются при исследовании движения космических аппаратов, баллистических ракет. В случае если рассматривается движение ЛА с умеренными скоростями V£ 2000¸3000 м/с в малой окрестности поверхности Земли, то Землю заменяют МГП. В этом случае горизонтальный полет на постоянной высоте считается прямолинейным. В других моделях Земли горизонтальный полет на постоянной высоте не является прямолинейным и будет иметь вид (рис.2).

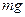Для реализации горизонтального полета в безвоздушном пространстве около сферы приближенно действует (без учета влияния других планет и Солнца) одна физическая сила земного притяжения ЛА, являющаяся центростремительной силой и в противоположном направлении- -фиктивная центробежная сила. Из условия равновесия получаем

 

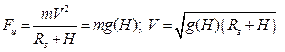
У поверхности Земли: Н=0, R_з=6371000 м, g₀=9,81 м/с², имеем V₀»7,9км/с=7900м/с.

Атмосфера становится исчезающе малой на высотах Н ³ 100-115 км. В этом случае для спутника на высоте круговой орбиты Н = 100 км значение скорости определим как:

 

.

 

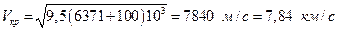Эта скорость называется круговой или первой космической.

Схематически траектории полёта в зависимости от величины начальной скорости V в начальной точке при угле наклона траектории q = 0 можно изобразить в следующем виде (рис.3).

Если то скорость называется параболическая или вторая космическая. При этой скорости ЛА уходит из сферы притяжения Земли. Иногда эту скорость называют «скоростью ухода». При V_гип > V_пар скорости называют гиперболическими, используемыми для дальних космических полётов. В случае V < V_кр траектории становятся приближённо эллиптическими (без учёта влияния атмосферы Земли).

В различных эллиптических траекториях центр масс Земли располагается в эксцентриситете эллипса. Эллипсы, пересекающие поверхность Земли, могут использоваться для описания движения баллистических ракет.

Расчеты показывают, что для

 

Земли: V_кр = 7,9 км/с; V_пар = 11,2 км/с;

 

Луны: V_кр = 1,7 км/с; V_пар = 2,4 км/с;

 

Марса: V_кр = 3,5 км/с; V_пар = 5 км/с.

 

Венеры: V_кр = 7,2 км/с; V_пар = 10.2 км/с.

На рис. 4 изображено распределение температуры воздуха в атмосфере Земли

На рис.5 показано распределение плотности воздуха в атмосфере Земли r₀ и b выбирается в зависимости от исследуемого диапазона высот Н₀ и Н

 

Рис. 4

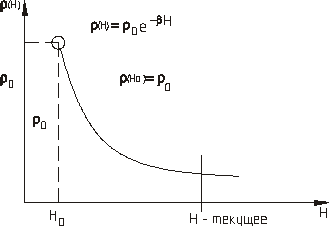Рис. 5

 

У поверхности Земли

Лекция 2.

ЛА можно разделить на составляющие, которые участвуют в создании аэродинамических сил и моментов. Наибольшую долю в создании подъемной силы обычно дает крыло. Суммарные силы и моменты всего ЛА складываются из сил и моментов его составляющих частей с учетом взаимного влияния (интерференции).

Рассмотрим сначала теоретические основы и предположения (гипотезы), на основе которых можно вывести соотношения для сил и момента изолированного крыла.

Исторически аэродинамика малых скоростей основывалась на постулате Н.Е. Жуковского (1847 - 1921) и С.А. Чаплыгина (1869 - 1942). Согласно этому постулату, точка схода воздушного потока, обтекающего крыло, фиксируется около задней кромки.

Это хорошо подтверждается экспериментально при плавном (безотрывном) ламинарном обтекании профиля крыла. С помощью этого постулата удалось определить значение подъемной силы крыла аналитически.

 

 

Вторая важная гипотеза и на ее основе теория пограничного слоя разработана немецким ученым А. Прандтлем. Согласно этой гипотезе вязкость (внутреннее трение) воздуха проявляется только в узком слое (пограничном слое), непосредственно примыкающем к поверхности обтекаемого крыла (см. рис. 7).

На рис. 8 а, б изображены картины обтекания крыльев на различных скоростях полета.

Рис. 7	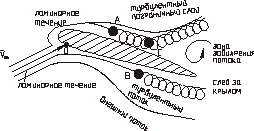Рис. 8а
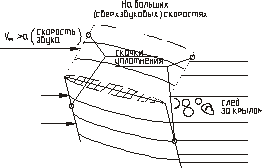Рис. 8б	О- точка критическая 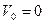А, В – точки перехода ламинарного пограничного слоя в турбулентный. С – точка отрыва пограничного слоя.   Скачки уплотнения – поверхности, где скачком изменяются давление и скорость потока. При этом возникает дополнительное сопротивление профиля (крыла), которое называют волновым сопротивлением.

Наименьшее сопротивление профиля возникает при ламинарном течении потока. Турболизация потока вызывает увеличение сопротивления трения и уменьшение подъемной силы крыла.

Дополнительные потери возникают при отрыве пограничного слоя на верхней поверхности крыла, которые обычно появляются на больших углах обтекания профиля крыла.

Рассмотрим уравнение (интеграл) Бернулли с целью объяснения причин изменения параметров воздушного потока при обтекании крыла. Бернулли, ученый швейцарского происхождения, состоявший членом Петербургской Академии Наук, применил закон сохранения энергии к двигающейся жидкости (газа) внутри трубопровода с переменным сечением (рис. 9).

Рис.9

Обозначим:

 

dF₁, dF₂ – площади сечений 1, 2;

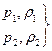давления и массовые плотности в сечениях 1, 2;

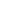
массы 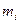в сечениях 1, 2.

Если пренебречь изменением внутренней тепловой энергии и внутренними потерями, то можно для несжимаемой жидкости записать сумму

трех видов энергий и считать эту величину постоянной

,

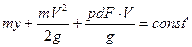где: 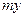- потенциальная энергия,

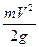- кинетическая энергия,

- потенциальная энергия давления (работа сил давления).

Поделив и умножив на третью составляющую, будем иметь:

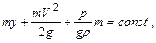
или, поделив на m слева и справа, получим уравнение Бернулли (уравнение напоров)

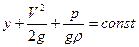. (3.1)

Рассмотрим (3.1) для двух расчетных сечений, умножив предварительно на

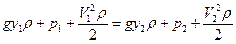, (3.2)

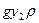-аэростатическое давление; p₂- статическое давление;

- динамическое давление. Часто обозначают:-скоростной напор.

Пример 1 (см. рис. 10).

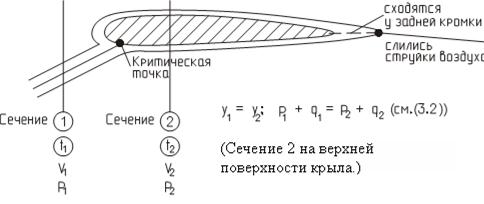
Рис. 10

Откуда . По гипотезе (постулату) Жуковского-Чаплыгина V₂>V₁ и q₂>q₁, т.е. 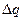>0, получаем >0 и p₁>p₂, т.е. на верхней поверхности крыла (профиля) давление понижается по сравнению с давлением набегающего потока 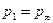.