И построение на их основе замкнутой систем управления
Синтез наблюдателей состояния
Наблюдатель состояния объекта управления по существу является подстраиваемой моделью этого объекта. Причём эту модель можно сформировать в удобных для синтеза регулятора состояния координатах. Технически наблюдатель состояния (НС) реализуется, как правило, в виде подпрограммы алгоритма управления, т.е. применение наблюдателя не приводит к техническому усложнению системы управления.
Таким образом, наблюдатель состоит из модели объекта управления
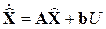, (4.27)
где X– вектор наблюдаемых (вычисляемых) координат объекта;
A, b – коэффициентные матрицы, взятые из описания динамики объекта (см.(3.7));
U – управляющее воздействие, которое подаётся на объект и одновременно через АЦП – преобразователь на его модель (наблюдатель).
Подстройки этой модели осуществляется в функции ошибки наблюдения, которая определяется, как разность между доступным для измерения выходным сигналом объекта управления и выходным сигналом с модели:
. (4.28)
Объединяя выражения (4.26) и (4.27) единую замкнутую систему через коэффициентную матрицу подстройки L получим уравнение полного наблюдателя состояния:
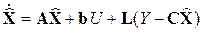. (4.29)
После приведения подобных членов получим описание наблюдателя состояния объекта в следующем виде
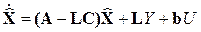, (4.30)
где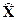 
– вектор оценки состояния объекта; L – матрица коэффициентов подстройки вектора оценок.
Как видно из (4.29), если начальное состояние наблюдателя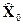 
и состояние объекта 
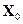отличаются, то под действием отрицательной обратной связи ошибка наблюдения будет стремиться к нулю. Таким образом осуществится подстройка модели объекта (4.27), и значение её внутренних координат после окончания переходного процесса подстройки будут совпадать со значениями ответствующих внутренних координат объекта. Строго говоря, наблюдатель (4.29) является наблюдателем начальных условий.
Из (4.30) следует (см. 3.26), что собственное движение процесса подстройки наблюдателя определяется выражением
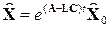. (4.31)
Из (4.31) следует, что выбором коэффициентов матрицы L можно обеспечить требуемый вид переходных процессов подстройки наблюдателя.
Использование наблюдателя, как уже отмечалось, позволяет отказаться от датчиков внутренних координат объекта, когда установка этих датчиков не возможна или не целесообразна. Например, все координаты состояния электропривода (ток, скорость, угол), в принципе, изменяемы. Однако, при микропроцессорном управлении число датчиков необходимо свести до минимума. Кроме того, для повышения качества регулировании часто требуется определять динамическую и статическую составляющие тока. Поэтому в данном случае целесообразно использовать наблюдатель.
Развернутая структурная схема замкнутой системы «объект управления + наблюдатель состояния + регулятор состояния» (ОУ+НС+РС), соответствующая схеме на рис. 4.1. в, представлена на рис. 4.6.
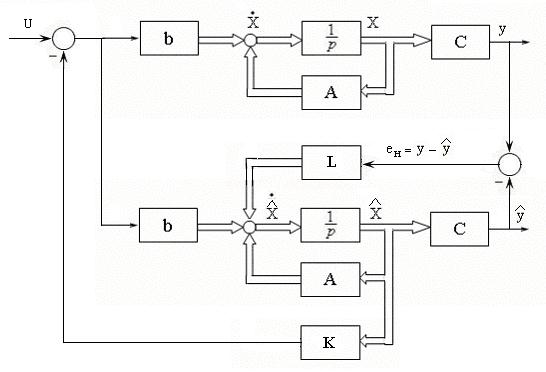
Рис. 4.6. Система управления с наблюдателем и регулятором состояния (с динамическим РС)
Регулятор состояния с наблюдателем называют также динамическим наблюдателем. Очевидно, что дополнительное включения наблюдателя будет влиять на общую динамику системы, увеличивая длительность переходных процессов по сравнению с длительностью этих процессов в системе с регулятором состояния без наблюдателя. Поэтому необходимо при расчете системы ОУ+РС+НС одновременно рассчитывать коэффициенты матриц и Ки L.
Задача расчета упрощается благодаря свойству разделимости процессов управления и наблюдения. Это можно доказать следующим образом. Вектор отклонений координат состояния наблюдателя от координат состояния объекта
,
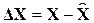в соответствии со структурной схемой на рис. 4.6. определяется следующей системой дифференциальных уравнений, представленных в матричной форме,
.
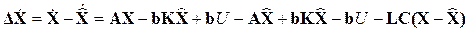Или после приведения подобных членов получим
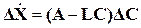. (4.32)
Учитывая, что
,
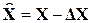свободное движение будет описываться следующим уравнением
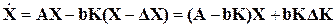. (4.33)
Уравнения (4.32) и (4.33) представим в единой матричной форме,
которая будет описывать свободное движение системы ОУ+НС+РС, :
.
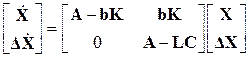Следовательно, характеристическое уравнение замкнутой системы будет
.
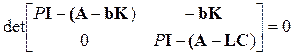Откуда получим, что характеристическое уравнение будет равно произведению характеристического уравнения системы ОУ+РС и характеристического уравнения НС
.
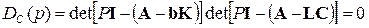Отсюда следует, что это уравнение можно представить в виде двух самостоятельных характеристических уравнений:
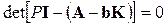(4.34)
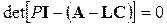(4.35)
Это дает возможность независимо синтезировать регулятор состояния без учета наличия наблюдателя состояния и синтезировать отдельно наблюдатель состояния. Но общее время переходных процессов в системе ОУ+НС+РС будет определяться совокупностью корней обоих уравнений (4.34) и (4.35). Поэтому коэффициенты матрицы L необходимо выбирать из условия, чтобы свободное движение наблюдателя было в 3¸5 раза быстрее, чем в системе ОУ+РС. В этом случае наличие наблюдателя увеличивает общую длительность переходных процессов в пределах 20 %.
Другое замечательное свойство, которое используется при синтезе наблюдателя, называется дуальностью процессов управления и наблюдения.
В уравнении (4.30) в отличие от уравнения системы с регулятором состояния (4.12) известная матрица С является матрицей-строкой, а искомая матрица L – матрицей-столбцом (в (4.12) искомая матрица К – это матрица-строка). Для того чтобы применить для определения матриц настройки наблюдателя состояния L методику для определения матрицы коэффициентов регулятора состояния К воспользуемся свойством, что транспонируемая матрица имеет тоже самое характеристическое уравнение, что и исходная матрица. Благодаря этому свойству
,
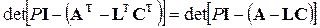где Т – знак транспонирования
СТ – матрица-столбец;
LТ – матрица-строка.
Отсюда следует, что если взять объект управления
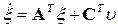
и регулятор состояния
,
то определение коэффициентов матрицы подстройки наблюдателя Lприводится к задаче определения для системы
элементов матрицы LТ как коэффициентов регулятора состояния.
Рассмотрим синтез НС по данной методике для системы управления электроприводом. Наблюдатель будет иметь второй порядок, т.к. выходной измеряемой координатой является скорость – х2, и координату х1 из описания объекта можно исключить. С другой стороны, для идентификации возмущающего воздействия (момента нагрузки на электродвигатель) расширим эту модель, подключив дополнительное интегрирующее звено к точке, где должно быть приложено это воздействие. Такой наблюдатель называется астатическим вследствие наличия интегратора в контуре подстройки.
На выходе дополнительного интегратора после процесса подстройки появится сигнал, равный величине возмущающего воздействия.
Вводя обозначение iH = x4, согласно (3.12) получается следующее описание объекта:
, (4.36)
,
где а24 = h2.
Коэффициентные матрицы сопряженной системы будут следующими:
. (4.37)
Задаемся эталонной матрицей АЭ вида (4.17) с биноминальной формой коэффициентов характеристического уравнения.
Подстановкой (4.37) в (4.22) определяются прямая и обратная преобразующие матрицы
. (4.38)
Регулятор, обеспечивающий матрице А-СТLT те же собственные значения, какие имеет эталонная матрица, может быть определен из уравнения, аналогичного (4.21)
. (4.39)
Подставляя (4.17), (4.37) и (4.38) в уравнение (4.39), получаем
.
Путем решения этого матричного уравнения определяются элементы матрицы L
. (4.40)
Наблюдатель незначительно влияет на время переходных процессов, если собственные значения матриц (А-ВК) и (A-LC) не пересекаются. Следовательно, при биномиальной форме коэффициентов характеристического уравнения АЭ это требование сводится к неравенству
,
где 
– собственное значение матрицы 
, кратное трем.
Данное условие является ограничением 
снизу. Ограничение сверху определяется из условия эффективности фильтрации шумов. Исходя из этих предпосылок, величина берется обычно в 3 ¸ 5 раз больше 
.
Подстановка в (4.40) из (4.9) и (4.18) значений коэффициентов, выраженных через , и параметров двигателя дает следующие выражения для элементов матрицы L:
.
В результате получаем структуру системы с регулятором состояния и наблюдателем, которая представлена на рис. 4.7. В объект, в отличие от структуры на рис. 4.5, включены силовой преобразователь с коэффициентом передачи КП и датчик скорости с коэффициентом КД. Соответственно коэффициенты обратных связей и коррекции наблюдателя изменяют свои значения:
.
Синтезированный наблюдатель позволяет дополнительно улучшить динамику системы регулирования по отношению к внешнему возмущающему воздействию, т.к. это воздействие идентифицируется. На рисунке 4.7 штриховой линией показана компенсирующая связь по току нагрузки 
.
Рис. 4.7. Структурная схема астатической системы управления скоростью двигателя с регулятором состояния и наблюдателем
При дискретном описании объекта уравнение дискретного наблюдателя по аналогии с уравнением непрерывного наблюдателя(4.30) будет иметь следующий вид
. (4.41)
Уравнение сопряженной системы, с помощью которой определяется матрица подстройки L, как и для непрерывной модели будет иметь вид
. (4.42)
Учитывая, что
,
свободное движение сопряженной системы определяется уравнением
. (4.43)
Эталонная дискретная модель свободного движения определяется следующей зависимостью
. (4.44)
Если координатные базисы моделей (4.42) и (4.44) совпадают, то матрица подстройки наблюдателя определяется из равенства матриц динамики моделей
или 
.
При несовпадении базисов их следую путем линейного преобразования
,
тогда
,
и матрица подстройки наблюдателя будет определяться из уравнения
. (4.45)
Рассмотрим определение матрицы L при аппроксимации дискретных моделей по Эйлеру. Переходная матрица системы (4.41), аппроксимированная по Эйлеру, так же как и в случае синтеза регулятора состояния, будет определяться следующим выражением:
.
Для переходной эталонной матрицы
.
Из равенства этих матриц следует, что
. (4.46)
Выражение (4.46) отличается от выражения (4.39) только тем, что его правая часть умножена на скалярную величину Т. Следовательно, при использовании дискретной модели, аппроксимированной по Эйлеру, элементы матрицы подстройки наблюдателя могут определяться по непрерывной модели с последующим умножением каждого элемента на величину периода квантования.
Объединение уравнений дискретного регулятора и дискретного наблюдателя дает алгоритмы непосредственного микропроцессорного управления объектом (в частности, электродвигателем) в области малых отклонений. Для получения рекурсивного алгоритма уравнение наблюдателя (4.41) разобьем на две составляющие: уравнение получения априорной оценки вектора состояний, обозначаемого через X0,
, (4.47)
и уравнение непосредственного наблюдателя (или уравнение подстройки оценки)
. (4.48)
Запишем уравнение определения ошибки регулирования
, (4.49)
и уравнение регулятора
. (4.50)
Рис. 4.7. Блок-схема алгоритма регулятора состояния и наблюдателя
На рис. 4.8 представлена блок-схема алгоритма, объединяющая уравнения регулятора состояния и наблюдателя.
Действие алгоритма происходит следующим образом. Предварительно производится опрос измерительных (блок 2) и управляющих (блок 1) устройств. На первом шаге производится присвоение начальных условий вектору оценки состояния (блок 3 и 4). На следующих шагах производится по уравнению (4.48) определение наблюдаемых координат (блок 5) на основе априорной оценки, полученной на предыдущем шаге (блок 9, уравнение (4.47)), и измеренной на данном шаге выходной координаты (блок 2). Далее определяются ошибка управления (блок 6, уравнение (4.49)) и управляющее воздействие (блок 7, уравнение (4.50)), которое выдается на исполнительное устройство (блок 8).
Данный алгоритм удовлетворяет требованиям к алгоритмам непосредственного микропроцессорного управления:
1. Параметры модели объекта прямо связаны с легко измеряемыми и легко вычисляемыми координатами объекта.
2. Параметры регулятора вычисляются по параметрам модели процесса без итераций и максимально простым способом.
3. Вычисления, связанные с управлением, производятся в темпе поступления данных.