Синтез регулятора состояния

Объединяя уравнения, описывающие динамику объекта (4.5) управления и регулятора состояния (4.11), получим уравнения, описывающие замкнутую систему с регулятором состояния:

 

. (4.12)

Если матрица М неособая, матричная передаточная функция системы (4.12) в соответствии с формулой (3.21) имеет вид:

, (4.13)

где - характеристическое уравнение замкнутой системы.

 

Из (4.13) следует, что с помощью матрицы обратных связей можно формировать требуемый вид собственных движений замкнутой системы, т.к. матрица К влияет на расположение полюсов. С помощью матрицы прямых связей М можно формировать вынужденное движение, т.к. данная матрица влияет на коэффициенты усиления и распределения нулей.

Наиболее конструктивным методом является синтез регулятора состояния на основе задания эталонной модели, исходя из требуемых качеств переходных процессов. Задача формируется в общем виде следующим образом. С помощью регулятора состояния

, (4.14)

требуется обеспечить такое собственное движение замкнутой системы с объектом управления

, (4.15)

где b – матрица-столбец; U – скалярная величина,

какое имеет эталонная модель

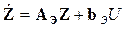. (4.16)

Вследствие того, что регулятор (4.14) изменяет только полюса передаточной функции объекта (4.15), такое управление часто называют модальным, т.е. управление осуществляется составляющими (модами) свободного движения замкнутой системы регулирования.

Матрица коэффициентов обратных связей определяется из условия равенства собственной матрицы замкнутой системы и собственной матрицы эталонной модели А_Э. Для решения этого уравнения необходимо, чтобы структуры синтезируемой системы и эталонной модели были одни и те же. Наиболее просто по требуемому виду характеристического уравнения (4.2) эталонная модель представляется в канонической форме управляемости, или в нормальной форме (см. Приложение 2)

. (4.17)

 

Коэффициенты а_Э0, а_Э1, …, а_Эn-1 определяются из характеристического уравнения (4.2), которому соответствует заданный вид переходного процесса. В частности, для получения апериодического процесса, как уже было отмечено, необходимо, чтобы собственные значения матрицы А_Э были действительными и равны между собой (см. Приложение 3).

Например, характеристическое уравнение системы третьего порядка имеет следующую биноминальную стандартную форму

, (4.18)

где а_Э2 = 3q, а_Э1 = 3q², а_Э0 = q³.

 

Величина q определяется, исходя, например, из длительности переходного процесса t_П:

. (4.19)

Если объект управления и эталонная модель описаны в разных внутренних переменных (координатных базисах), то, как было показано в параграфе 3.2, для согласования структур объекта и эталонной модели необходимо осуществить линейное преобразование координат

Х=PZ, (4.20)

где Р – неособая квадратная преобразующая матрица.

 

После преобразования (4.20) система «объект (4.15) + регулятор (4.14)» относительно нового координатного базиса пространства состояний примет следующий вид (см. также выражение (3.18))

 

или

.

 

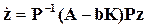Из условия равенства собственных движений синтезируемой системы и эталонной модели следует, что

,

откуда

. (4.21)

Преобразующая матрица Р и обратная ей матрица Р^-1 находятся следующим образом (см. Приложение 2):

P_n=b; P_n-i=AP_n-i+1 + a_n-iP_n, (4.22)

где Р_n – столбцы матрицы Р; а_n-I – коэффициенты характеристического уравнения матрицы .

 

Рассмотрим пример синтез системы регулирования двигателем постоянного тока при использовании непрерывной модели (3.11) и (3.12). Согласно (3.23)

. (4.23)

 

Используя выражения (4.22) и правило обращения матриц (см. Приложение 1), определим прямую и обратную матрицы линейного преобразования координатного базиса для согласования эталонной модели и модели описания динамики электродвигателя

 

. (4.24)

 

Подстановка матриц (3.12), (4.17), (4.24) в матричное уравнение (4.21) даёт следующее выражение

 

.

 

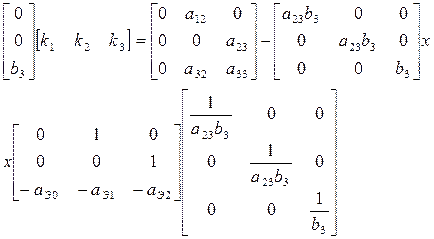Из этого уравнения, которое достаточно просто решается, получаем выражения для коэффициентов РС:

 

. (4.25)

 

С учетом (3.11) и (4.18) получаем выражения для определения коэффициентов РС через параметры электродвигателя и значения среднегеометрического корня q эталонного характеристического уравнения:

k₁ = C_eТ_ЯТ_Мq³; k₂ = C_e(3Т_ЯТ_Мq² - 1); k₃ = R(3T_Яq - 1).

 

Структурная схема стабилизации скорости двигателя с астатическими регулятором состояния представлена на рис. 4.5.

 

 

Рис. 4.5. Структурная схема системы астатического управления

скоростью двигателя, построенная на основе регулятора состояния

 

Для дискретной модели объекта переходная матрица замкнутой системы определяется выражением (см. (3.26))

.

Переходная матрица эталонной дискретной модели по аналогии определяется следующим образом

.

Элементы матрицы (коэффициенты) обратных связей К вычисляются исходя из равенства. После подстановки получается следующее матричное уравнение для определения коэффициентов РС

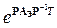= . (4.26)

Как правило, эту задачу решают численным способом, используя стандартные или специально разработанные компьютерные программы.

Для упрощения решения матричного уравнения (4.26) аналитическим методом воспользуемся приближенными выражениями для определения матриц динамики дискретной модели объекта и эталонной модели. С этой целью разложим, используя формулу (3.27), в степенной ряд экспоненциальные функции от матриц и удержим первые два слагаемых. В результате получим

.

Точность такой аппроксимации напрямую зависит от величины периода квантования T. Как правило, при определении величины Т из условий, представленных в сгруппированном виде в (1.59), такая аппроксимация

является достаточно корректной. По существу такая линейная аппроксимация соответствует численному интегрированию методом Эйлера первого порядка. Известным недостатком такого метода является быстрое накопление по мере движения по шагам приращения аргумента ошибки вычисления. Однако в рассматриваемом случае такого накопления ошибки вычисления не происходи из-за наличия отрицательной обратной связи в замкнутой системе управления.

Из равенства ,

следует, что .

Это уравнение полностью совпадает с уравнением (4.21), полученным для определения коэффициентов непрерывного РС.

Таким образом, мы пришли к интересному выводу, что при линейной аппроксимации дискретной модели объекта (аппроксимация по Эйлеру), расчет коэффициентов дискретного РС можно вести по формулам, полученным для определения коэффициентов непрерывного РС.